Advertisements
Advertisements
Question
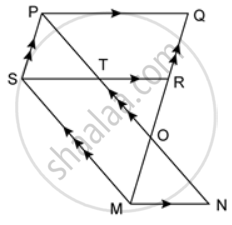
In the given figure, PQRS is a parallelogram in which PA = AB = Prove that: SA ‖ QB and SA = QB.
Solution
Construction:
Join BS and AQ.
Join diagonal QS.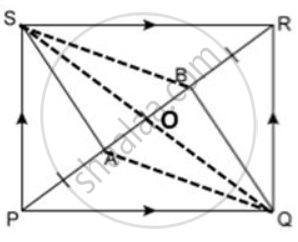
Since diagonals of a parallelogram bisect each other.
∴ OP = OR and OQ = OS
Also, PA = AB = BR
Now, OP = OR and PA = PB
⇒ OP - PA = OR - PB
⇒ OA = OB
Thus, in quadrilateral SAQB, we have
OQ = OS and OA = OB
⇒ Diagonals of a quadrilateral SAQB bisect each other.
⇒ SAQB is a parallelogram.
⇒ SA || QB
⇒SA = QB. ...(Opposite sides are equal)
APPEARS IN
RELATED QUESTIONS
ABCD is a parallelogram. P and Q are mid-points of AB and CD. Prove that APCQ is also a parallelogram.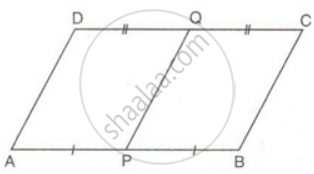
Prove that if the diagonals of a parallelogram are equal then it is a rectangle.
PQRS is a parallelogram. T is the mid-point of RS and M is a point on the diagonal PR such that MR = `(1)/(4)"PR"`. TM is joined and extended to cut QR at N. Prove that QN = RN.
Prove that the line segment joining the mid-points of the diagonals of a trapezium is parallel to each of the parallel sides, and is equal to half the difference of these sides.
In a parallelogram PQRS, M and N are the midpoints of the opposite sides PQ and RS respectively. Prove that
PMRN is a parallelogram.
In a parallelogram PQRS, M and N are the midpoints of the opposite sides PQ and RS respectively. Prove that
MN bisects QS.
ABCD is a trapezium in which side AB is parallel to side DC. P is the mid-point of side AD. IF Q is a point on the Side BC such that the segment PQ is parallel to DC, prove that PQ = `(1)/(2)("AB" + "DC")`.
In the given figure, PQRS is a trapezium in which PQ ‖ SR and PS = QR. Prove that: ∠PSR = ∠QRS and ∠SPQ = ∠RQP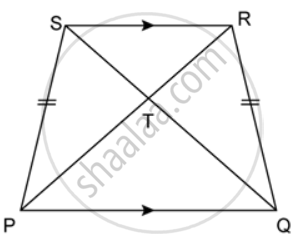
Prove that the diagonals of a kite intersect each other at right angles.
In the given figure, PQ ∥ SR ∥ MN, PS ∥ QM and SM ∥ PN. Prove that: ar. (SMNT) = ar. (PQRS).