Advertisements
Advertisements
Question
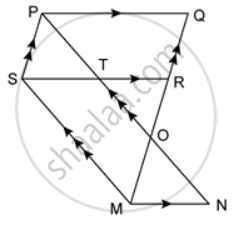
PQRS is a parallelogram. T is the mid-point of RS and M is a point on the diagonal PR such that MR = `(1)/(4)"PR"`. TM is joined and extended to cut QR at N. Prove that QN = RN.
Solution
Join PR to intersect QS at O
Diagonals of a parallelogram bisect each other.
Therefore, OP = OR
But MR = `(1)/(4)"PR"`
∴ MR = `(1)/(4)(2 xx "QR")`
⇒ MR = `(1)/(2)"OR"`
Hence, M is the mid-point of OR.
In ΔROS, T and M are the mid-points of RS and OR respectively.
Therefore, TM || OS
⇒ TN || QS
Also in ΔRQS, T is the mid-point of RS and TN || QS
Therefore, N is the mid-point of QR and TN = `(1)/(2)"QS"`
⇒ QN = RN.
APPEARS IN
RELATED QUESTIONS
ABCD is a parallelogram. P and Q are mid-points of AB and CD. Prove that APCQ is also a parallelogram.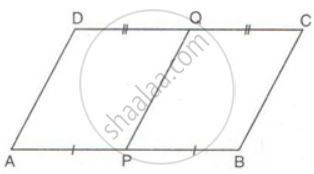
SN and QM are perpendiculars to the diagonal PR of parallelogram PQRS.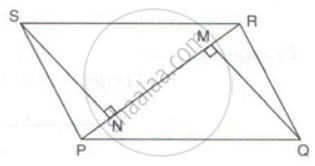
Prove that:
(i) ΔSNR ≅ ΔQMP
(ii) SN = QM
PQRS is a parallelogram. PQ is produced to T so that PQ = QT. Prove that PQ = QT. Prove that ST bisects QR.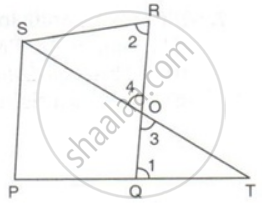
Prove that if the diagonals of a parallelogram are equal then it is a rectangle.
In a parallelogram PQRS, M and N are the midpoints of the opposite sides PQ and RS respectively. Prove that
RN and RM trisect QS.
ABCD is a trapezium in which side AB is parallel to side DC. P is the mid-point of side AD. IF Q is a point on the Side BC such that the segment PQ is parallel to DC, prove that PQ = `(1)/(2)("AB" + "DC")`.
In the given figure, PQRS is a trapezium in which PQ ‖ SR and PS = QR. Prove that: ∠PSR = ∠QRS and ∠SPQ = ∠RQP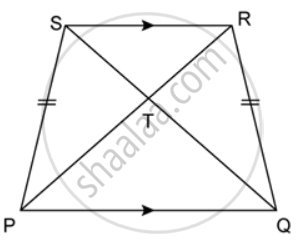
Prove that the diagonals of a kite intersect each other at right angles.
The diagonals AC and BC of a quadrilateral ABCD intersect at O. Prove that if BO = OD, then areas of ΔABC an ΔADC area equal.
In the given figure, PQ ∥ SR ∥ MN, PS ∥ QM and SM ∥ PN. Prove that: ar. (SMNT) = ar. (PQRS).