Advertisements
Advertisements
Question
Prove that the quadrilateral formed by joining the mid-points of consecutive sides of a rhombus is a rectangle.
Solution
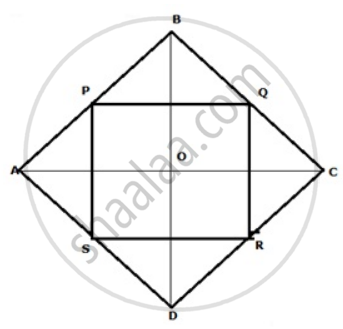
In ΔABC, P and Q are mid points of sides AB and BC respectively.
Therefore, PQ || AC and PQ = `(1)/(2)"AC"`(using mid-point theorem) ...(1)
In ΔADC
R and S are the mid points of CD and AD respectively
Therefore, RS || AC and RS = `(1)/(2)"AC"`(using mid-point theorem) ...(2)
From equations (1) and (2), we have
PQ || RS and PQ = RS
As in quadrilateral PQRS one pair of opposite sides are equal and parallel to each other, so, it is a parallelogram.
Let diagonals of rhombus ABCD intersects each other at point O.
Now in quadrilateral OMQN
MQ || ON ...(PQ || AC)
QN || OM ...(QR || BD)
So, OMQN is parallelogram
∠MQN = ∠NOM
∠PQR = ∠NOM
But, ∠NOM = 90° ...(diagonals of a rhombus are perpendicular to each other)
∠PQR = 90°
Clearly PQRS is a parallelogram having one of its interior angle as 90°.
Hence, PQRS is rectangle.
APPEARS IN
RELATED QUESTIONS
In the following figure, ABCD is a rhombus and DCFE is a square.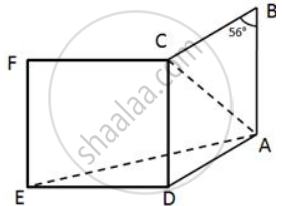
If ∠ABC =56°, find:
(i) ∠DAE
(ii) ∠FEA
(iii) ∠EAC
(iv) ∠AEC
Prove that the quadrilateral formed by joining the mid-points of consecutive sides of a rectangle is a rhombus.
Prove that if the diagonals of a quadrilateral bisect each other at right angles then it is a rhombus.
Prove that the area of a rhombus is equal to half the rectangle contained by its diagonals.
Diagonals of a rhombus are equal and perpendicular to each other.
A rhombus can be constructed uniquely if both diagonals are given.
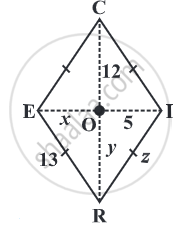
The diagonals of a rhombus are 8 cm and 15 cm. Find its side.
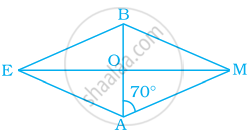
In rhombus BEAM, find ∠AME and ∠AEM.