Question

प्रारम्भ में x-अक्ष के अनुदिश v_x चाल से गति करती हुई, दो आवेशित प्लेटों के मध्य क्षेत्र में m द्रव्यमान तथा -q आवेश का एक कण प्रवेश करता है। प्लेटों की लम्बाई L है। इन दोनों प्लेटों के बीच एकसमान विद्युत-क्षेत्र E बनाए रखा जाता है। दर्शाइए कि प्लेट के अन्तिम किनारे पर कण का ऊर्ध्वाधर विक्षेप \[\ce{\frac{qE{L}^{2}}{2m{v}_{x}^{2}}}\] है।

Answer 1

एकसमान विद्युत-क्षेत्र में आवेशित कण (इलेक्ट्रॉन) का गमन-पथ- (i) जब कण का प्रारम्भिक वेग विद्युत-क्षेत्र की दिशा के लम्बवत् है- माना धातु की दो समान्तर प्लेटें जिन पर विपरीत आवेश हैं, एक-दूसरे से कुछ दूरी पर स्थित हैं। इन प्लेटों के बीच के स्थान में विद्युत-क्षेत्र एकसमान है। माना ऊपरी प्लेट धनावेशित है, जबकि नीचे की प्लेट ऋणावेशित है। अत: विद्युत-क्षेत्र E कागज के तल में नीचे की ओर दिष्ट होगा।

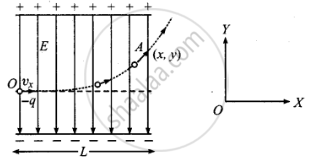
माना कोई कण जिस पर आवेश - q है तथा जो x अक्ष के अनुदिश गतिमान है, v_x वेग से विद्युत क्षेत्र E में प्रवेश करता है चूँकि विद्युत क्षेत्र Y अक्ष की ऋणात्मक दिशा में नीचे की ओर है; अतः कण पर y अक्ष के अनुदिश लगने वाला बल F_y = qE

कण पर x अक्ष के अनुदिश कोई बल कार्य नहीं करेगा।

माना कण का द्रव्यमान m है , तब इस बल के कारण कण की गति में उत्पन्न त्वरण `"a"_"y" = "F"_"y"/"m" = "qE"/"m"`

चूँकि कण का X-अक्ष के अनुदिश प्रारम्भिक वेग v_x तथा त्वरण शून्य है, अतः X-अक्ष के अनुदिश t सेकण्ड में चली गयी दूरी

x = v_xt       .....(1)

चूँकि कण का Y-अक्ष के अनुदिश प्रारम्भिक वेग 0 तथा त्वरण a_y है, अतः Y-अक्ष के अनुदिश t सेकण्ड में चली गयी दूरी

y = `1/2"a"_"y" "t"^2 = 1/2 ("qE"/"m")(x/"v"_x)   ....[because "t" = x/"v"_x]`

अतः y = `("qE"/(2"mv"_x^2))x^2`

यह समीकरण y = cx² के समरूप है तथा परवलय को प्रकट करती है अतः विद्युत क्षेत्र में अभिलम्बवत प्रवेश करने वाले आवेशित कण का गमन पथ परबलयाकार होता है। 

माना कण प्लेटों के बीच के क्षेत्र को बिन्दु पर छोड़ता है, तब

बिन्दु A के लिए     x = L    (∵ प्लेटों की लम्बाई = L)

पथ के समीकरण में मान रखने पर,

y = `("qE"/(2"m""v"_x^2))"L"^2 = ("qEL"^2)/(2"mv"_x^2)` 

अतः प्लेटों के दूसरे किनारे पर कण का ऊध्वाधर विक्षेप `("qEL"^2)/(2"mv"_x^2)` होगा।