Advertisements
Advertisements
प्रश्न
Prove that 5`sqrt(2)` is irrational.
उत्तर
Let 5`sqrt(2)` is a rational number.
∴ 5`sqrt(2) = p/q` , where p and q are some integers and HCF(p, q) = 1 …(1)
⇒5√2q = p
⇒(5`sqrt (2) q)^2 = p^2`
⇒` 2(25q^2) = p^2`
⇒ `p^2 `is divisible by 2
⇒ p is divisible by 2 ….(2)
Let p = 2m, where m is some integer.
∴5`sqrt(2)` 𝑞 = 2m
⇒(5`sqrt(2) q )^2 = (2m)^2`
⇒` 2(25 q^2) = 4m^2`
⇒`25q ^2 = 2m^2`
⇒` q^ 2 `is divisible by 2
⇒ q is divisible by 2 ….(3)
From (2) and (3) is a common factor of both p and q, which contradicts (1).
Hence, our assumption is wrong.
Thus, 5`sqrt(2)` is irrational.
APPEARS IN
संबंधित प्रश्न
Give two rational numbers lying between 0.232332333233332... and 0.212112111211112.
Find two irrational numbers between 0.5 and 0.55.
Find two irrational numbers lying between 0.1 and 0.12.
Prove that of the numbers `sqrt (6) ` is irrational:
Given universal set =
`{ -6, -5 3/4, -sqrt4, -3/5, -3/8, 0, 4/5, 1, 1 2/3, sqrt8, 3.01, π, 8.47 }`
From the given set, find: set of rational numbers
The product of a non-zero rational and an irrational number is ______.
Classify the following number as rational or irrational with justification:
`- sqrt(0.4)`
Find three rational numbers between `5/7` and `6/7`
Show that x is irrational, if x2 = 27.
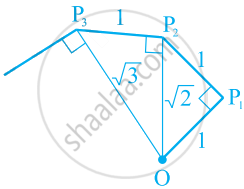
Classroom activity (Constructing the ‘square root spiral’): Take a large sheet of paper and construct the ‘square root spiral’ in the following fashion. Start with a point O and draw a line segment OP1 of unit length. Draw a line segment P1 P2 perpendicular to OP1 of unit length. Now draw a line segment P2 P3 perpendicular to OP2. Then draw a line segment P3 P4 perpendicular to OP3. Continuing in this manner, you can get the line segment Pn–1Pn by drawing a line segment of unit length perpendicular to OPn–1. In this manner, you will have created the points P2, P3,...., Pn,.... ., and joined them to create a beautiful spiral depicting `sqrt2, sqrt3, sqrt4,` ...