Advertisements
Advertisements
प्रश्न
Prove the theorem of perpendicular axes.
(Hint: Square of the distance of a point (x, y) in the x–y plane from an axis through the origin perpendicular to the plane is x2 + y2).
उत्तर १
The theorem of perpendicular axes states that the moment of inertia of a planar body (lamina) about an axis perpendicular to its plane is equal to the sum of its moments of inertia about two perpendicular axes concurrent with the perpendicular axis and lying in the plane of the body.
A physical body with centre O and a point mass m,in the x–y plane at (x, y) is shown in the following figure.
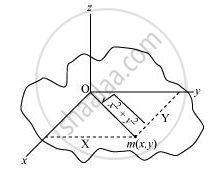
Moment of inertia about x-axis, Ix = mx2
Moment of inertia about y-axis, Iy = my2
Moment of inertia about z-axis, Iz = `m(sqrt(x^2 + y^2))^2`
Ix + Iy = mx2 + my2
= m(x2 + y2)
`= m(sqrt(x^2 + y^2))`
`I_x + I_y = I_z`
Hence the theorem is proved
उत्तर २
The theorem of perpendicular axes: According to this theorem, the moment of inertia of a plane lamina (i.e., a two dimensional body of any shape/size) about any axis OZ perpendicular to the plane of the lamina is equal to sum of the moments of inertia of the lamina about any two mutually perpendicular axes OX and OY in the plane of lamina, meeting at a point where the given axis OZ passes through the lamina. Suppose at the point ‘R’ m{ particle is situated moment of inertia about Z axis of lamina
= moment of inertia of body about r-axis
= moment of inertia of the body about y-axis.

APPEARS IN
संबंधित प्रश्न
Find the radius of gyration of circular ring of radius r about a line perpendicular to the plane of the ring and passing through one of its particles.
Answer in brief:
State the conditions under which the theorems of parallel axes and perpendicular axes are applicable. State the respective mathematical expressions.
A solid cylinder of radius r and mass M rolls down an inclined plane of height h. When it reaches the bottom of the plane, then its rotational kinetic energy is ____________.
(g = acceleration due to gravity)
When a 12000 joule of work is done on a flywheel, its frequency of rotation increases from 10 Hz to 20 Hz. The moment of inertia of flywheel about its axis of rotation is ______. (π2 = 10)
The moment of inertia of a uniform square plate about an axis perpendicular to its plane and passing through the centre is `"Ma"^2/6` where M is the mass and 'a' is the side of square plate. Moment of inertia of this plate about an axis perpendicular to its plane and passing through one of its corner is ______.
From a disc of radius R and mass M, a circular hole of diameter R, whose rim passes through the centre is cut. What is the moment of inertia of the remaining part of the disc about a perpendicular axis, passing through the centre?
A metal ring has a moment of inertia 2 kg·m2 about a transverse axis through its centre. It is melted and recast into a thin uniform disc of the same radius. What will be the disc's moment of inertia about its diameter?
A uniform disc of mass 10 kg and radius 60 cm rotates about an axis perpendicular to its plane and passing through its centre at 1200 rpm. Calculate its rotation kinetic energy. [Take π2 = 10]
State and prove the theorem of the parallel axis about the moment of inertia.
Prove the theorem of perpendicular axes about the moment of inertia.
