Advertisements
Advertisements
Question
Prove the theorem of perpendicular axes.
(Hint: Square of the distance of a point (x, y) in the x–y plane from an axis through the origin perpendicular to the plane is x2 + y2).
Solution 1
The theorem of perpendicular axes states that the moment of inertia of a planar body (lamina) about an axis perpendicular to its plane is equal to the sum of its moments of inertia about two perpendicular axes concurrent with the perpendicular axis and lying in the plane of the body.
A physical body with centre O and a point mass m,in the x–y plane at (x, y) is shown in the following figure.
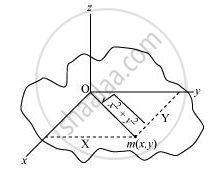
Moment of inertia about x-axis, Ix = mx2
Moment of inertia about y-axis, Iy = my2
Moment of inertia about z-axis, Iz = `m(sqrt(x^2 + y^2))^2`
Ix + Iy = mx2 + my2
= m(x2 + y2)
`= m(sqrt(x^2 + y^2))`
`I_x + I_y = I_z`
Hence the theorem is proved
Solution 2
The theorem of perpendicular axes: According to this theorem, the moment of inertia of a plane lamina (i.e., a two dimensional body of any shape/size) about any axis OZ perpendicular to the plane of the lamina is equal to sum of the moments of inertia of the lamina about any two mutually perpendicular axes OX and OY in the plane of lamina, meeting at a point where the given axis OZ passes through the lamina. Suppose at the point ‘R’ m{ particle is situated moment of inertia about Z axis of lamina
= moment of inertia of body about r-axis
= moment of inertia of the body about y-axis.

APPEARS IN
RELATED QUESTIONS
Prove the theorem of parallel axes.
(Hint: If the centre of mass is chosen to be the origin `summ_ir_i = 0`
Find the radius of gyration of circular ring of radius r about a line perpendicular to the plane of the ring and passing through one of its particles.
State and explain the theorem of parallel axes.
When a 12000 joule of work is done on a flywheel, its frequency of rotation increases from 10 Hz to 20 Hz. The moment of inertia of flywheel about its axis of rotation is ______. (π2 = 10)
A circular disc 'X' of radius 'R' made from iron plate of thickness 't' has moment of inertia 'Ix' about an axis passing through the centre of disc and perpendicular to its plane. Another disc 'Y' of radius '3R' made from an iron plate of thickness `("t"/3)` has moment of inertia 'Iy' about the s same as that of disc X. The relation between Ix and ly is ______.
Two bodies have their moments of inertia I and 2I respectively about their axes of rotation. If their kinetic energies of rotation are equal, their angular momenta will be in the ratio ______.
The moment of inertia of a uniform square plate about an axis perpendicular to its plane and passing through the centre is `"Ma"^2/6` where M is the mass and 'a' is the side of square plate. Moment of inertia of this plate about an axis perpendicular to its plane and passing through one of its corner is ______.
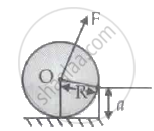
A uniform cylinder of mass M and radius R is to be pulled over a step of height a (a < R) by applying a force F at its centre 'O' perpendicular to the plane through the axes of the cylinder on the edge of the step (see figure). The minimum value of F required is:
A metal ring has a moment of inertia 2 kg·m2 about a transverse axis through its centre. It is melted and recast into a thin uniform disc of the same radius. What will be the disc's moment of inertia about its diameter?
Prove the theorem of perpendicular axes about the moment of inertia.
