Advertisements
Advertisements
Question
Prove the theorem of parallel axes.
(Hint: If the centre of mass is chosen to be the origin `summ_ir_i = 0`
Advertisements
Solution
Theorem of parallel axes: According to this theorem, moment of inertia of a rigid body about any axis AB is equal to moment of inertia of the body about another axis KL passing through centre of mass C of the body in a direction parallel to AB, plus the product of total mass M of the body and square of the perpendicular distance between the two parallel axes. If h is perpendicular distance between the axes AB and KL, then Suppose the rigid body is made up of n particles m1, m2, …. mn, mn at perpendicular distances r1, r2, ri…. rn. respectively from the axis KL passing through the centre of mass C of the body.
If h is the perpendicular distance of the particle of mass m{ from KL, then
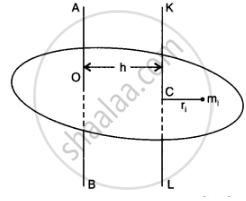
The perpendicular distance of ith particular from the axis
`AB = (r_i + n)`
or `I_(AB) = sum_(i)m_i(r_i + h)^2`
`= sum_(i) m_ir_i^2 + sum_(i) m_ih^2 + 2h sum_(i) m_ir_i` ....(ii)
As the body is balanced about the centre of mass the algebraic sum of the moments of the weights of all particles about an axis passing through C must be zero
`sum_(i)(m_ig)r_i = 0 or g sum_(i) m_ir_i` or `sum_(i) m_ir_i = 0` ...(iii)
From equation (ii) we have
`I_(AB) = sum_(i) m_ir_i^2 + (summ_i)h^2 + 0`
or `I_(AB) = I_(KL) + Mh^2`
Where `I_"KL" = sum_(i) m_ir_i^2` and `M = sum m_i`
RELATED QUESTIONS
State the theorem of perpendicular axes about moment of inertia.
Prove the theorem of parallel axes about moment of inertia
State Brewster's law.
Prove the theorem of perpendicular axes.
(Hint: Square of the distance of a point (x, y) in the x–y plane from an axis through the origin perpendicular to the plane is x2 + y2).
Find the radius of gyration of circular ring of radius r about a line perpendicular to the plane of the ring and passing through one of its particles.
Answer in brief:
State the conditions under which the theorems of parallel axes and perpendicular axes are applicable. State the respective mathematical expressions.
When a 12000 joule of work is done on a flywheel, its frequency of rotation increases from 10 Hz to 20 Hz. The moment of inertia of flywheel about its axis of rotation is ______. (π2 = 10)
A circular disc 'X' of radius 'R' made from iron plate of thickness 't' has moment of inertia 'Ix' about an axis passing through the centre of disc and perpendicular to its plane. Another disc 'Y' of radius '3R' made from an iron plate of thickness `("t"/3)` has moment of inertia 'Iy' about the s same as that of disc X. The relation between Ix and ly is ______.
A wheel of moment of inertia 2 kg m2 is rotating at a speed of 25 rad/s. Due to friction on the axis, it comes to rest in 10 minutes. Total work done by friction is ______.
The moment of inertia of a uniform square plate about an axis perpendicular to its plane and passing through the centre is `"Ma"^2/6` where M is the mass and 'a' is the side of square plate. Moment of inertia of this plate about an axis perpendicular to its plane and passing through one of its corner is ______.
A solid sphere of mass 'M' and radius 'R' is rotating about its diameter. A disc of same mass and radius is also rotating about an axis passing through its centre and perpendicular to the plane but angular speed is twice that of the sphere. The ratio of kinetic energy of disc to that of sphere is ______.
Two particles A and B having equal charges are placed at a distance d apart. A third charged particle placed on the perpendicular bisection of AB at distance x. The third particle experiences maximum force when ______.
A uniform disc of mass 10 kg and radius 60 cm rotates about an axis perpendicular to its plane and passing through its centre at 1200 rpm. Calculate its rotation kinetic energy. [Take π2 = 10]
State and prove the theorem of the parallel axis about the moment of inertia.
Prove the theorem of perpendicular axes about the moment of inertia.
