Advertisements
Advertisements
Question
Prove the result that the velocity v of translation of a rolling body (like a ring, disc, cylinder or sphere) at the bottom of an inclined plane of a height h is given by `v^2 = (2gh)/((1+k^2"/"R^2))`.
Using dynamical consideration (i.e. by consideration of forces and torques). Note k is the radius of gyration of the body about its symmetry axis, and R is the radius of the body. The body starts from rest at the top of the plane.
Advertisements
Solution 1
A body rolling on an inclined plane of height h is shown in the following figure:
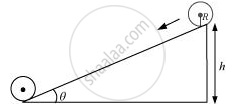
m = Mass of the body
R = Radius of the body
K = Radius of gyration of the body
v = Translational velocity of the body
h =Height of the inclined plane
g = Acceleration due to gravity
Total energy at the top of the plane, E1= mgh
Total energy at the bottom of the plane, `E_b = KE_rot + KE_trans`
`=1/2 Iomega^2 + 1/2 mv^2`
But `I = mk^2 " and " omega = v/r`
`:.E_b = 1/2 (mk^2)(v^2/R_2) + 1/2 mv^2`
`=1/2 mv^2 k^2/R^2 + 1/2mv^2`
`= 1/2 mv^2(1+ k^2/R^2)`
From the law of conservation of energy, we have:
`E_T = E_b`
`mgh = 1/2mv^2(1+k^2/R^2)`
`:.v = (2gh)/(1+k^2"/"R^2)`
Hence, the given result is proved.
Solution 2
Let a rolling body (I = Mk2) rolls down an inclined plane with an initial velocity u = 0; When it reaches the bottom of the inclined plane, let its linear velocity be v. Then from conservation of mechanical energy, we have Loss in P.E. = Gain in translational K.E. + Gain in rotational K.E.
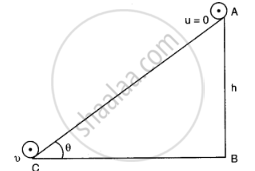
`Mgh = 1/2mv^2 + 1/2 Iomega^2`
`= 1/2mv^2 + 1/2(mk^2)(v^2/R^2)`
`Mgh = 1/2mv^2 (1+k^2/R^2)`
`v^2 = (2gh)/(1+k^2/R^2)`
RELATED QUESTIONS
Derive an expression for kinetic energy, when a rigid body is rolling on a horizontal surface without slipping. Hence find kinetic energy for a solid sphere.
A solid sphere rolls down two different inclined planes of the same heights but different angles of inclination. (a) Will it reach the bottom with the same speed in each case? (b) Will it take longer to roll down one plane than the other? (c) If so, which one and why?
Read each statement below carefully, and state, with reasons, if it is true or false;
The instantaneous speed of the point of contact during rolling is zero.
A solid sphere of mass 1 kg rolls on a table with linear speed 2 m/s, find its total kinetic energy.
A stone of mass 2 kg is whirled in a horizontal circle attached at the end of 1.5m long string. If the string makes an angle of 30° with vertical, compute its period. (g = 9.8 m/s2)
A hollow sphere and a solid sphere having same mss and same radii are rolled down a rough inclined plane.
A sphere can roll on a surface inclined at an angle θ if the friction coefficient is more than \[\frac{2}{7}g \tan\theta.\] Suppose the friction coefficient is \[\frac{1}{7}g\ tan\theta.\] If a sphere is released from rest on the incline, _____________ .
The following figure shows a smooth inclined plane fixed in a car accelerating on a horizontal road. The angle of incline θ is related to the acceleration a of the car as a = g tanθ. If the sphere is set in pure rolling on the incline, _____________.
A cylinder rolls on a horizontal place surface. If the speed of the centre is 25 m/s, what is the speed of the highest point?
Discuss the interlink between translational, rotational and total kinetic energies of a rigid object rolls without slipping.
A pendulum consisting of a massless string of length 20 cm and a tiny bob of mass 100 g is set up as a conical pendulum. Its bob now performs 75 rpm. Calculate kinetic energy and increase in the gravitational potential energy of the bob. (Use π2 = 10)
A disc of the moment of inertia Ia is rotating in a horizontal plane about its symmetry axis with a constant angular speed ω. Another disc initially at rest of moment of inertia Ib is dropped coaxially onto the rotating disc. Then, both the discs rotate with the same constant angular speed. The loss of kinetic energy due to friction in this process is, ______
The speed of a solid sphere after rolling down from rest without sliding on an inclined plane of vertical height h is, ______
A uniform disc of mass 100g has a diameter of 10 cm. Calculate the total energy of the disc when rolling along with a horizontal table with a velocity of 20 cms-1. (take the surface of the table as reference)
A solid sphere rolls down from top of inclined plane, 7m high, without slipping. Its linear speed at the foot of plane is ______. (g = 10 m/s2)
The power (P) is supplied to rotating body having moment of inertia 'I' and angular acceleration 'α'. Its instantaneous angular velocity is ______.
The angular velocity of minute hand of a clock in degree per second is ______.
A uniform disc of radius R, is resting on a table on its rim.The coefficient of friction between disc and table is µ (Figure). Now the disc is pulled with a force F as shown in the figure. What is the maximum value of F for which the disc rolls without slipping?
Solid spherical ball is rolling on a frictionless horizontal plane surface about is axis of symmetry. The ratio of rotational kinetic energy of the ball to its total kinetic energy is ______.
