Question

Prove the result that the velocity v of translation of a rolling body (like a ring, disc, cylinder or sphere) at the bottom of an inclined plane of a height h is given by `v^2 = (2gh)/((1+k^2"/"R^2))`.

Using dynamical consideration (i.e. by consideration of forces and torques). Note k is the radius of gyration of the body about its symmetry axis, and R is the radius of the body. The body starts from rest at the top of the plane.

Answer 1

A body rolling on an inclined plane of height h is shown in the following figure:

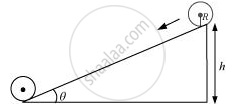
m = Mass of the body

R = Radius of the body

K = Radius of gyration of the body

v = Translational velocity of the body

h =Height of the inclined plane

g = Acceleration due to gravity

Total energy at the top of the plane, E­₁= mgh

Total energy at the bottom of the plane, `E_b = KE_rot + KE_trans`

`=1/2 Iomega^2 + 1/2 mv^2`

But `I = mk^2 " and " omega = v/r`

`:.E_b = 1/2 (mk^2)(v^2/R_2) + 1/2 mv^2`

`=1/2 mv^2 k^2/R^2 + 1/2mv^2`

`= 1/2 mv^2(1+ k^2/R^2)`

From the law of conservation of energy, we have:

`E_T = E_b`

`mgh = 1/2mv^2(1+k^2/R^2)`

`:.v = (2gh)/(1+k^2"/"R^2)`

Hence, the given result is proved.

Answer 2

Let a rolling body (I = Mk²) rolls down an inclined plane with an initial velocity u = 0; When it reaches the bottom of the inclined plane, let its linear velocity be v. Then from conservation of mechanical energy, we have Loss in P.E. = Gain in translational K.E. + Gain in rotational K.E.

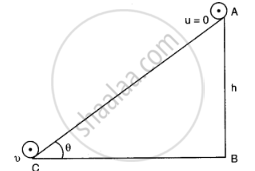
`Mgh = 1/2mv^2 + 1/2 Iomega^2`

`= 1/2mv^2 + 1/2(mk^2)(v^2/R^2)`

`Mgh = 1/2mv^2 (1+k^2/R^2)`

`v^2 = (2gh)/(1+k^2/R^2)`