Advertisements
Advertisements
प्रश्न
Answer in Brief:
A rigid object is rolling down an inclined plane derive the expression for the acceleration along the track and the speed after falling through a certain vertical distance.
उत्तर

The figure shows a rigid object of mass M and radius R, rolling down an inclined plane, without slipping. Inclination of the plane with the horizontal is θ. As the objects starts rolling down, its gravitational P.E. is converted into K.E. of rolling. Starting from rest, let v be the speed of the centre of mass as the object comes down through a vertical distance h. If the frictional force on the body is large enough, the body rolls without slipping.
v = Linear speed of the centre of mass
R = Radius of the body
ω = Angular speed of rotation of the body, `therefore omega="v"/R` for any particle
M = Mass of the body
K = Radius of gyration of the body `therefore I=MK^2`
Total kinetic energy of rolling = Translational K.E. + Rotational K.E.
`E = 1/2M"v"^2+1/2Iomega^2 = 1/2 M"v"^2 [1 + K^2/R^2]`
`therefore E=Mgh = 1/2 M"v"^2 [1 + K^2/R^2]`
`therefore "v" = sqrt((2gh)/[1 + K^2/R^2])`
Linear distance travelled along the plane is `s = h/sintheta`
During this distance, the linear velocity has increased from zero to v. If `a` is the linear acceleration along the plane,
`2as = "v"^2-u^2 therefore 2a(h/sintheta) = (2gh)/[1 + K^2/R^2]-0`
`therefore a=(gsintheta)/[1 + K^2/R^2]`
For pure sliding, without friction, the acceleration is `gsintheta` and final velocity is `sqrt(2gh)`. Thus, during pure rolling, the factor `[1 + K^2/R^2]` is effective for both the expressions.
APPEARS IN
संबंधित प्रश्न
Derive an expression for kinetic energy, when a rigid body is rolling on a horizontal surface without slipping. Hence find kinetic energy for a solid sphere.
A solid sphere rolls down two different inclined planes of the same heights but different angles of inclination. (a) Will it reach the bottom with the same speed in each case? (b) Will it take longer to roll down one plane than the other? (c) If so, which one and why?
Prove the result that the velocity v of translation of a rolling body (like a ring, disc, cylinder or sphere) at the bottom of an inclined plane of a height h is given by `v^2 = (2gh)/((1+k^2"/"R^2))`.
Using dynamical consideration (i.e. by consideration of forces and torques). Note k is the radius of gyration of the body about its symmetry axis, and R is the radius of the body. The body starts from rest at the top of the plane.
Read each statement below carefully, and state, with reasons, if it is true or false;
The instantaneous speed of the point of contact during rolling is zero.
Read each statement below carefully, and state, with reasons, if it is true or false;
For perfect rolling motion, work done against friction is zero.
Read each statement below carefully, and state, with reasons, if it is true or false;
A wheel moving down a perfectly frictionless inclined plane will undergo slipping (not rolling) motion
A solid sphere of mass 1 kg rolls on a table with linear speed 2 m/s, find its total kinetic energy.
If a rigid body of radius ‘R’ starts from rest and rolls down an inclined plane of inclination
‘θ’ then linear acceleration of body rolling down the plane is _______.
A stone of mass 2 kg is whirled in a horizontal circle attached at the end of 1.5m long string. If the string makes an angle of 30° with vertical, compute its period. (g = 9.8 m/s2)
Two uniform solid spheres having unequal masses and unequal radii are released from rest from the same height on a rough incline. If the spheres roll without slipping, ___________ .
A hollow sphere and a solid sphere having same mss and same radii are rolled down a rough inclined plane.
A sphere cannot roll on
In rear-wheel drive cars, the engine rotates the rear wheels and the front wheels rotate only because the car moves. If such a car accelerates on a horizontal road the friction
(a) on the rear wheels is in the forward direction
(b) on the front wheels is in the backward direction
(c) on the rear wheels has larger magnitude than the friction on the front wheels
(d) on the car is in the backward direction.
The following figure shows a smooth inclined plane fixed in a car accelerating on a horizontal road. The angle of incline θ is related to the acceleration a of the car as a = g tanθ. If the sphere is set in pure rolling on the incline, _____________.
A cylinder rolls on a horizontal place surface. If the speed of the centre is 25 m/s, what is the speed of the highest point?
A hollow sphere is released from the top of an inclined plane of inclination θ. (a) What should be the minimum coefficient of friction between the sphere and the plane to prevent sliding? (b) Find the kinetic energy of the ball as it moves down a length l on the incline if the friction coefficient is half the value calculated in part (a).
A solid sphere of mass 0⋅50 kg is kept on a horizontal surface. The coefficient of static friction between the surfaces in contact is 2/7. What maximum force can be applied at the highest point in the horizontal direction so that the sphere does not slip on the surface?
Discuss the interlink between translational, rotational and total kinetic energies of a rigid object rolls without slipping.
A pendulum consisting of a massless string of length 20 cm and a tiny bob of mass 100 g is set up as a conical pendulum. Its bob now performs 75 rpm. Calculate kinetic energy and increase in the gravitational potential energy of the bob. (Use π2 = 10)
The speed of a solid sphere after rolling down from rest without sliding on an inclined plane of vertical height h is, ______
What is the condition for pure rolling?
What is the difference between sliding and slipping?
A solid sphere rolls down from top of inclined plane, 7m high, without slipping. Its linear speed at the foot of plane is ______. (g = 10 m/s2)
A solid sphere of mass 1 kg and radius 10 cm rolls without slipping on a horizontal surface, with velocity of 10 emfs. The total kinetic energy of sphere is ______.
A man is supported on a frictionless horizontal surface. It is attached to a string and rotates about a fixed centre at an angular velocity `omega`. The tension in the strings is F. If the length of string and angular velocity are doubled, the tension in string is now ____________.
The power (P) is supplied to rotating body having moment of inertia 'I' and angular acceleration 'α'. Its instantaneous angular velocity is ______.
A ring and a disc roll on horizontal surface without slipping with same linear velocity. If both have same mass and total kinetic energy of the ring is 4 J then total kinetic energy of the disc is ______.
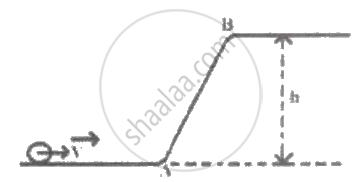
A solid sphere is rolling on a frictionless surface with translational velocity 'V'. It climbs the inclined plane from 'A' to 'B' and then moves away from Bon the smooth horizontal surface. The value of 'V' should be ______.
A 1000 kg car has four 10 kg wheels. When the car is moving, fraction of total K.E. of the car due to rotation of the wheels about their axles is nearly (Assume wheels be uniform disc)
An object is rolling without slipping on a horizontal surface and its rotational kinetic energy is two-thirds of translational kinetic energy. The body is ______.
A solid spherical ball rolls on an inclined plane without slipping. The ratio of rotational energy and total energy is ______.
A circular disc reaches from top to bottom of an inclined plane of length 'L'. When it slips down the plane, it takes time ' t1'. when it rolls down the plane, it takes time t2. The value of `t_2/t_1` is `sqrt(3/x)`. The value of x will be ______.
Solid spherical ball is rolling on a frictionless horizontal plane surface about is axis of symmetry. The ratio of rotational kinetic energy of the ball to its total kinetic energy is ______.
The least coefficient of friction for an inclined plane inclined at angle α with horizontal in order that a solid cylinder will roll down without slipping is ______.
A solid sphere of mass 2 kg is rolling on a frictionless horizontal surface with velocity 6m/s. It collides on the free end of an ideal spring whose other end is fixed. The maximum compression produced in the spring will be ______.
(Force constant of the spring = 36 N/m)
The kinetic energy and angular momentum of a body rotating with constant angular velocity are E and L. What does `(2E)/L` represent?
The angular displacement of a particle in 6 sec on a circle with angular velocity `pi/3` rad/sec is ______.
When a sphere rolls without slipping, the ratio of its kinetic energy of translation to its total kinetic energy is ______.
A disc of mass 4 kg rolls on a horizontal surface. If its linear speed is 3 m/ s, what is its total kinetic energy?
