Advertisements
Advertisements
प्रश्न
Prove the theorem of parallel axes.
(Hint: If the centre of mass is chosen to be the origin `summ_ir_i = 0`
उत्तर
Theorem of parallel axes: According to this theorem, moment of inertia of a rigid body about any axis AB is equal to moment of inertia of the body about another axis KL passing through centre of mass C of the body in a direction parallel to AB, plus the product of total mass M of the body and square of the perpendicular distance between the two parallel axes. If h is perpendicular distance between the axes AB and KL, then Suppose the rigid body is made up of n particles m1, m2, …. mn, mn at perpendicular distances r1, r2, ri…. rn. respectively from the axis KL passing through the centre of mass C of the body.
If h is the perpendicular distance of the particle of mass m{ from KL, then
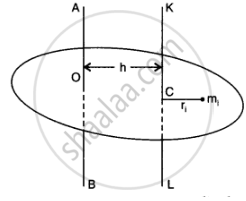
The perpendicular distance of ith particular from the axis
`AB = (r_i + n)`
or `I_(AB) = sum_(i)m_i(r_i + h)^2`
`= sum_(i) m_ir_i^2 + sum_(i) m_ih^2 + 2h sum_(i) m_ir_i` ....(ii)
As the body is balanced about the centre of mass the algebraic sum of the moments of the weights of all particles about an axis passing through C must be zero
`sum_(i)(m_ig)r_i = 0 or g sum_(i) m_ir_i` or `sum_(i) m_ir_i = 0` ...(iii)
From equation (ii) we have
`I_(AB) = sum_(i) m_ir_i^2 + (summ_i)h^2 + 0`
or `I_(AB) = I_(KL) + Mh^2`
Where `I_"KL" = sum_(i) m_ir_i^2` and `M = sum m_i`
APPEARS IN
संबंधित प्रश्न
State an expression for the moment of intertia of a solid uniform disc, rotating about an axis passing through its centre, perpendicular to its plane. Hence derive an expression for the moment of inertia and radius of gyration:
i. about a tangent in the plane of the disc, and
ii. about a tangent perpendicular to the plane of the disc.
State Brewster's law.
Prove the theorem of perpendicular axes.
(Hint: Square of the distance of a point (x, y) in the x–y plane from an axis through the origin perpendicular to the plane is x2 + y2).
Answer in brief:
State the conditions under which the theorems of parallel axes and perpendicular axes are applicable. State the respective mathematical expressions.
A string of length ℓ fixed at one end carries a mass m at the other. The string makes 2/π revolutions/sec around the vertical axis through the fixed end. The tension in the string is ______.
A circular disc 'X' of radius 'R' made from iron plate of thickness 't' has moment of inertia 'Ix' about an axis passing through the centre of disc and perpendicular to its plane. Another disc 'Y' of radius '3R' made from an iron plate of thickness `("t"/3)` has moment of inertia 'Iy' about the s same as that of disc X. The relation between Ix and ly is ______.
Two bodies have their moments of inertia I and 2I respectively about their axes of rotation. If their kinetic energies of rotation are equal, their angular momenta will be in the ratio ______.
The moment of inertia of a uniform square plate about an axis perpendicular to its plane and passing through the centre is `"Ma"^2/6` where M is the mass and 'a' is the side of square plate. Moment of inertia of this plate about an axis perpendicular to its plane and passing through one of its corner is ______.
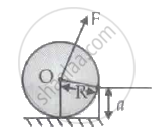
A uniform cylinder of mass M and radius R is to be pulled over a step of height a (a < R) by applying a force F at its centre 'O' perpendicular to the plane through the axes of the cylinder on the edge of the step (see figure). The minimum value of F required is:
State and prove the theorem of the parallel axis about the moment of inertia.
