Advertisements
Advertisements
प्रश्न
Read the following axioms:
- Things which are equal to the same thing are equal to one another.
- If equals are added to equals, the wholes are equal.
- Things which are double of the same thing are equal to one another.
Check whether the given system of axioms is consistent or inconsistent.
उत्तर
Some of Euclid’s axioms are
- Things which are equal to the same thing are equal to one another.
- If equals are added to equals, the wholes are equal.
- Things which are double of the same things are equal to one another.
Thus, given three axioms are Euclid’s axioms. So, here we cannot deduce any statement from these axioms which contradicts any axiom. So, given system of axioms is consistent.
APPEARS IN
संबंधित प्रश्न
In how many points two distinct planes can intersect?
The number of dimensions, a solid has ______.
Euclid divided his famous treatise “The Elements” into ______.
Boundaries of surfaces are ______.
Pythagoras was a student of ______.
Euclid stated that all right angles are equal to each other in the form of ______.
Attempts to prove Euclid’s fifth postulate using the other postulates and axioms led to the discovery of several other geometries.
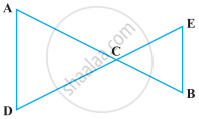
Solve the following question using appropriate Euclid’s axiom:
In the following figure, we have AB = BC, BX = BY. Show that AX = CY.
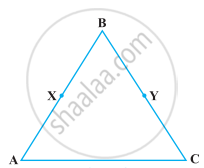
Solve the following question using appropriate Euclid’s axiom:
In the following figure, we have BX = `1/2` AB, BY = `1/2` BC and AB = BC. Show that BX = BY.
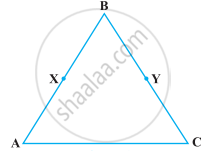
Solve the following question using appropriate Euclid’s axiom:
In the following figure, we have AC = DC, CB = CE. Show that AB = DE.