Advertisements
Advertisements
प्रश्न
Represent `sqrt3.5,` `sqrt9.4,` `sqrt10.5` on the real number line.
Advertisements
उत्तर
We are asked to represent the real numbers `sqrt3.5,` `sqrt9.4` and `sqrt10.5`on the real number line
We will follow a certain algorithm to represent these numbers on real number line
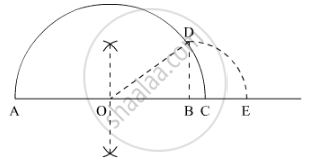
(a) `sqrt3.5`
We will take A as reference point to measure the distance
(1) Draw a sufficiently large line and mark a point A on it
(2) Take a point B on the line such that AB = 3.5 cm
(3) Mark a point C on the line such that BC = 1 cm
(4) Find mid point of AB and let it be O
(5) Take O as center and OC as radius and draw a semi circle. Draw a perpendicular BD which cuts the semi circle at D
(6) Take B as the center and BD as radius, draw an arc which cuts the horizontal line at E
(7) Point E is the representation of `sqrt3.5`
(b) `sqrt9.4`
We will take A as reference point to measure the distance. We will follow the same figure in the part (a)
(1) Draw a sufficiently large line and mark a point A on it
(2) Take a point B on the line such that AB = 9.4 cm
(3) Mark a point C on the line such that BC = 1 cm
(4) Find mid point of AB and let it be O
(5) Take O as center and OC as radius and draw a semi circle. Draw a perpendicular BC which cuts the semi circle at D
(6) Take B as the center and BD as radius, draw an arc which cuts the horizontal line at E
(7) Point E is the representation of `sqrt9.4`
(c) `sqrt10.5`
We will take A as reference point to measure the distance. We will follow the same figure in the part (a)
(1) Draw a sufficiently large line and mark a point A on
(2) Take a point B on the line such that AB = 10.5 cm
(3) Mark a point C on the line such that BC = 1 cm
(4) Find mid point of AB and let it be O
(5) Take O as center and OC as radius and draw a semi circle. Draw a perpendicular BC which cuts the semi circle at D
(6) Take B as the center and BD as radius, draw an arc which cuts the horizontal line at E
(7) Point E is the representation of `sqrt10.5`
APPEARS IN
संबंधित प्रश्न
Represent `sqrt6,` `sqrt7,` `sqrt8` on the number line.
The number 0.318564318564318564 ........ is:
The number \[1 . \bar{{27}}\] in the form \[\frac{p}{q}\] , where p and q are integers and q ≠ 0, is
\[23 . \bar{{43}}\] when expressed in the form \[\frac{p}{q}\] (p, q are integers q ≠ 0), is
\[0 . \bar{{001}}\] when expressed in the form \[\frac{p}{q}\] (p, q are integers, q ≠ 0), is
Represent the following numbers on the number line
`6.bar(4)` upto 3 decimal places
Represent the following number on the number line:
7.2
Represent the following number on the number line:
`(-3)/2`
Represent geometrically the following number on the number line:
`sqrt(4.5)`
Represent geometrically the following number on the number line:
`sqrt(5.6)`
