Advertisements
Advertisements
प्रश्न
Show that electric potential at a point P, at a distance 'r' from a fixed point charge Q, is given by:
`v=(1/(4pi∈_0))Q/r`.
उत्तर
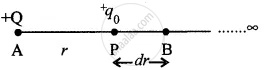
Let potential at point P is required due to a fixed point charge Q at A. Distance `bar(AP)`= r. Let us place a point test charge q0 at P. Let us consider a point B very near to P at a distance dr, such that \[ \overrightarrow{F_P} = \overrightarrow{F_B}\].
Force, \[\overrightarrow{F}\] between Q and q0 = `1/(4pi∈_0) -(Qxxq_0)/r^2`
where ∈0 = permittivity for free space
Now, work done in carrying the charge q0 from P to B is
`dW = -1/(4pi∈_0) (Qxxq_0)/r^2`.dr
The negative sign indicates negative work due to repulsion between Q and q0.
Similarly,
Work was done in carrying to infinity (∞),
W = `int dW=- int_r^∞ 1/(4pi∈_0). (Qxxq_0)/r^2`.dr
⇒ `W =-1/(4pi∈_0) .Qxxq_0` `" _r^∞r^-2`dr
⇒ `W = +1/(4pi∈_0) .Qxxq_0[1/r]_r^∞`
⇒ `W = +1/(4pi∈_0) .Qxxq_0[1/∞ ∼1/r]`
⇒ `W = -1/(4pi∈_0) .(Qxxq_0)/r`
When, the test charge, q0 is taken from ∞.
The work done is positive and magnitude remains the same.
∴ `W =1/(4pi∈_0) .(Qxxq_0)/r`
Since potential at P = `W/(q_0)`
∴ V. potential at P = `1/(4pi∈_0) .(Qxxq_0)/(r.q_0)`
`V = Q/(4pi∈_0.r) J C^-1 or V`
`V = (1/(4pi∈_0)).Q/r V`
APPEARS IN
संबंधित प्रश्न
Electric potential energy of two point charges q and q0 is ________.
If a positive charge moves opposite to the direction of the electric field, the field does _______ work on charge and potential energy ________.
It becomes possible to define potential at a point in an electric field because electric field ______.
From a point charge, there is a fixed point A. At A, there is an electric field of 500 V/m and potential difference of 3000 V. Distance between point charge and A will be ______.
-
The metal plate divides the capacitor into two capacitors connected in parallel to each other.
-
The metal plate divides the capacitors into two capacitors connected in series with each other.
-
The metal plate is equivalent to a dielectric of zero dielectric constant.
A test charge is moved from lower potential point to a higher potential point. The potential energy of test charge will ______.
An electric dipole of moment `vec"p"` is placed in a uniform electric field `vec"E"`. Then ______.
- the torque on the dipole is `vec"p" xx vex"E"`
- the potential energy of the system is `vec"p" * vec"E"`
- the resultant force on the dipole is zero.
Choose the correct option.
The force acting on a particle in one dimension is F = ax - 2xβ3. The corresponding potential energy V(x), assuming V(0) = 0 is given by ______.
If a conductor has a potential V ≠ 0 and there are no charges anywhere else outside, then ______.
- there must be charges on the surface or inside itself.
- there cannot be any charge in the body of the conductor.
- there must be charges only on the surface.
- there must be charges inside the surface.
The electric potential on the axis of an electric dipole at a distance ‘r from it’s centre is V. Then the potential at a point at the same distance on its equatorial line will be ______.
