Advertisements
Advertisements
प्रश्न
Show that the moment of inertia of a solid body of any shape changes with temperature as I = I0 (1 + 2αθ), where I0 is the moment of inertia at 0°C and α is the coefficient of linear expansion of the solid.
उत्तर
Given:
Coefficient of linear expansion of solid = α
Moment of inertia at 0 °C = I0
If temperature changes to θ from 0 °C, then change in temperature, (ΔT) =θ
Let I be the new moment of inertia attained due to rise in temperature.
Let R0 be the radius of gyration at 0 °C.
We know that on heating, radius of gyration will change as
R = R0(1 + αθ)
Here, R is the radius of gyration after heating.
I0 = MR02 , where M = mass of the body
Now, I = MR2 = MR02(1 + αθ)2
Expanding binomially and neglecting the higher terms of order (αθ) that will be very small, we get
I = MR02(1 + 2 αθ)
So, I = I0(1 + 2 αθ)
Hence, proved.
APPEARS IN
संबंधित प्रश्न
A hole is drilled in a copper sheet. The diameter of the hole is 4.24 cm at 27.0 °C. What is the change in the diameter of the hole when the sheet is heated to 227 °C? Coefficient of linear expansion of copper = 1.70 × 10–5 K–1.
If an automobile engine is overheated, it is cooled by pouring water on it. It is advised that the water should be poured slowly with the engine running. Explain the reason.
Is it possible for two bodies to be in thermal equilibrium if they are not in contact?
A system X is neither in thermal equilibrium with Y nor with Z. The systems Y and Z
A gas thermometer measures the temperature from the variation of pressure of a sample of gas. If the pressure measured at the melting point of lead is 2.20 times the pressure measured at the triple point of water, find the melting point of lead.
Answer the following question.
Derive the relation between three coefficients of thermal expansion.
Answer the following question.
State applications of thermal expansion.
A metal rod of Young's moduls 'Y' and coefficient of linear expansion 'a' has its temeprature raised by 'Δ θ'. The linear stress to prevent the expansion of rod is ______.
(L and l is original length of rod and expansion respectively)
A metal rod of cross-sectional area 3 × 10-6 m2 is suspended vertically from one end has a length 0.4 m at 100°C. Now the rod is cooled upto 0°C, but prevented from contracting by attaching a mass 'm' at the lower end. The value of 'm' is ______.
(Y = 1011 N/m2, coefficient of linear expansion = 10-5/K, g = 10m/s2)
The radius of a metal sphere at room temperature T is R, and the coefficient of linear expansion of the metal is α. The sphere is heated a little by a temperature ∆T so that its new temperature is T + ∆T. The increase in the volume of the sphere is approximately ______.
Find out the increase in moment of inertia I of a uniform rod (coefficient of linear expansion α) about its perpendicular bisector when its temperature is slightly increased by ∆T.
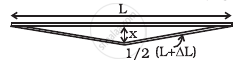
A rail track made of steel having length 10 m is clamped on a raillway line at its two ends (figure). On a summer day due to rise in temperature by 20° C, it is deformed as shown in figure. Find x (displacement of the centre) if αsteel = 1.2 × 10–5/°C.
At what temperature a gold ring of diameter 6.230 cm be heated so that it can be fitted on a wooden bangle of diameter 6.241 cm? Both diameters have been measured at room temperature (27°C). (Given: coefficient of linear thermal expansion of gold αL = 1.4 × 10-5 K-1).
Each side of a box made of metal sheet in cubic shape is 'a' at room temperature 'T', the coefficient of linear expansion of the metal sheet is 'α'. The metal sheet is heated uniformly, by a small temperature ΔT, so that its new temeprature is T + ΔT. Calculate the increase in the volume of the metal box.
If the length of a cylinder on heating increases by 2%, the area of its base will increase by ______.
The height of mercury column measured with brass scale at temperature T0 is H0. What height H' will the mercury column have at T = 0°C. Coefficient of volume expansion of mercury is γ. Coefficient of linear expansion of brass is α ______.
Given below are two statements: one is labelled as Assertion A and the other is labelled as Reason R.
- Assertion A: When a rod lying freely is heated, no thermal stress is developed in it.
- Reason R: On heating, the length of the rod increases. In light of the above statements.
choose the correct answer from the options given below:
A solid metallic cube having a total surface area of 24 m2 is uniformly heated. If its temperature is increased by 10°C, calculate the increase in the volume of the cube.
(Given: α = 5.0 × 10-4°C-1)
A clock with an iron pendulum keeps the correct time at 15°C. If the room temperature is 20°C, the error in seconds per day will be near ______.
(coefficient of linear expansion of iron is 1.2 × 10-5/°C)
