Advertisements
Advertisements
प्रश्न
Show that `lim_("n" -> oo) (1^2 + 2^2 + ... + (3"n")^2)/((1 + 2 + ... + 5"n")(2"n" + 3)) = 9/25`
उत्तर
`lim_("n" -> oo) (1^2 + 2^2 + ... + (3"n")^2)/((1 + 2 + ... + 5"n")(2"n" + 3)) = lim_("n" -> oo) ((3"n"(3"n" + 1)(2 xx 3"n" + 1))/6)/((5"n"(5"n" + 1))/2 (2"n" + 3))`
= `lim_("n" -> oo) (3"n"(3"n" + 1)(6"n" + 1) xx 2)/(6 xx 5"n"(5"n" + 1)(2"n" + 3))`
= `lim_("n" -> oo) ("n"(3"n" + 1)(6"n" + 1))/(5"n"(5"n" + 1)(2"n" + 3))`
= `lim_("n" -> oo) ("n"*"n"(3 + 1/"n") "n"(6 + 1/"n"))/(5"n"*"n"(5 + 1/"n") "n"*(2 + 3/"n"))`
= `lim_("n" -> oo) ("n"^3(3 + 1/"n")(6 + 1/"n"))/("n"^3*5(5 + 1/"n")(2 + 3/"n"))`
= `((3 + 0)(6 + 0))/(5(5 + 0)(2 + 0))`
= `18/50`
= `9/25`
APPEARS IN
संबंधित प्रश्न
Evaluate the following limit:
`lim_(z -> -3) [sqrt("z" + 6)/"z"]`
Evaluate the following limit:
`lim_(x -> 2)[(x^(-3) - 2^(-3))/(x - 2)]`
Evaluate the following limit :
`lim_(x -> 7) [(x^3 - 343)/(sqrt(x) - sqrt(7))]`
In the following example, given ∈ > 0, find a δ > 0 such that whenever, |x – a| < δ, we must have |f(x) – l| < ∈.
`lim_(x -> -3) (3x + 2)` = – 7
In the following example, given ∈ > 0, find a δ > 0 such that whenever, |x – a| < δ, we must have |f(x) – l| < ∈.
`lim_(x -> 2) (x^2 - 1)` = 3
In exercise problems 7 – 15, use the graph to find the limits (if it exists). If the limit does not exist, explain why?
`lim_(x -> 1) f(x)` where `f(x) = {{:(x^2 + 2",", x ≠ 1),(1",", x = 1):}`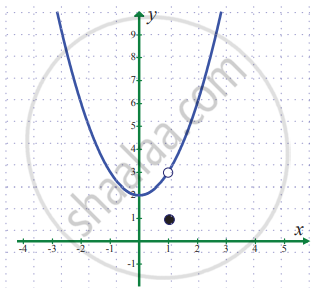
In exercise problems 7 – 15, use the graph to find the limits (if it exists). If the limit does not exist, explain why?
`lim_(x -> 1) sin pi x`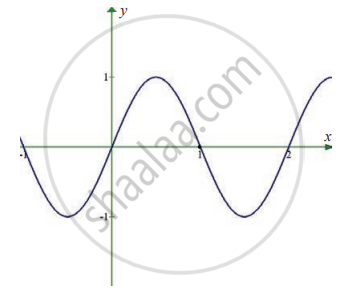
Evaluate the following limits:
`lim_(x -> 0) (sqrt(1 - x) - 1)/x^2`
Evaluate the following limits:
`lim_(x -> oo) (x^3 + x)/(x^4 - 3x^2 + 1)`
Evaluate the following limits:
`lim_(x -> oo) (1 + x - 3x^3)/(1 + x^2 +3x^3)`
Evaluate the following limits:
`lim_(x ->oo) (x^3/(2x^2 - 1) - x^2/(2x + 1))`
Evaluate the following limits:
`lim_(x -> 0) (sqrt(2) - sqrt(1 + cosx))/(sin^2x)`
Choose the correct alternative:
`lim_(x -> 0) ("a"^x - "b"^x)/x` =
Choose the correct alternative:
If `f(x) = x(- 1)^([1/x])`, x ≤ 0, then the value of `lim_(x -> 0) f(x)` is equal to
Choose the correct alternative:
If `lim_(x -> 0) (sin "p"x)/(tan 3x)` = 4, then the value of p is
If `lim_(x->1)(x^5-1)/(x-1)=lim_(x->k)(x^4-k^4)/(x^3-k^3),` then k = ______.
If `lim_(x -> 1) (x + x^2 + x^3|+ .... + x^n - n)/(x - 1)` = 820, (n ∈ N) then the value of n is equal to ______.
`lim_(x→-1) (x^3 - 2x - 1)/(x^5 - 2x - 1)` = ______.
