Advertisements
Advertisements
प्रश्न
Evaluate the following limits:
`lim_(x -> 0) (sqrt(2) - sqrt(1 + cosx))/(sin^2x)`
उत्तर
`lim_(x -> 0) ((sqrt(2) - sqrt(1 + cosx))/(sin^2x))`
= `lim_(x -> 0) ((sqrt(2) - sqrt(1 + cosx))(sqrt(2) + sqrt(1 + cosx)))/(sin^2x (sqrt(2) + sqrt(1 + cosx))`
= `lim_(x -> 0) (2 - (1 + cosx))/((1 - cos^2x)(sqrt(2) + sqrt(1 + cosx))`
= `lim_(x -> 0) (1 - cosx)/((1 +cosx)(1 - cosx)(sqrt(2) + sqrt(1 + cosx))`
= `lim_(x -> 0) 1/((1 + cosx)(sqrt(2) + sqrt(1 + cosx))`
= `1/((1 + cos0)(sqrt(2) + sqrt(1 + 1))`
= `1/(2(sqrt(2) + sqrt(2))`
=`1/(2 xx 2sqrt(2))`
`lim_(x -> 0) (sqrt(2) - sqrt(1 + cosx))/(sin^2x) = 1/(4sqrt(2))`
APPEARS IN
संबंधित प्रश्न
In the following example, given ∈ > 0, find a δ > 0 such that whenever, |x – a| < δ, we must have |f(x) – l| < ∈.
`lim_(x -> -3) (3x + 2)` = – 7
Evaluate the following :
Given that 7x ≤ f(x) ≤ 3x2 – 6 for all x. Determine the value of `lim_(x -> 3) "f"(x)`
In problems 1 – 6, using the table estimate the value of the limit
`lim_(x -> - 3) (sqrt(1 - x) - 2)/(x + 3)`
| x | – 3.1 | – 3.01 | – 3.00 | – 2.999 | – 2.99 | – 2.9 |
| f(x) | – 0.24845 | – 0.24984 | – 0.24998 | – 0.25001 | – 0.25015 | – 0.25158 |
In problems 1 – 6, using the table estimate the value of the limit
`lim_(x -> 0) sin x/x`
| x | – 0.1 | – 0.01 | – 0.001 | 0.001 | 0.01 | 0.1 |
| f(x) | 0.99833 | 0.99998 | 0.99999 | 0.99999 | 0.99998 | 0.99833 |
In problems 1 – 6, using the table estimate the value of the limit
`lim_(x -> 0) (cos x - 1)/x`
| x | – 0.1 | – 0.01 | – 0.001 | 0.0001 | 0.01 | 0.1 |
| f(x) | 0.04995 | 0.0049999 | 0.0004999 | – 0.0004999 | – 0.004999 | – 0.04995 |
In exercise problems 7 – 15, use the graph to find the limits (if it exists). If the limit does not exist, explain why?
`lim_(x -> 3) 1/(x - 3)`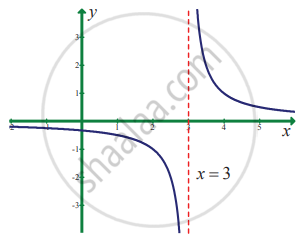
In exercise problems 7 – 15, use the graph to find the limits (if it exists). If the limit does not exist, explain why?
`lim_(x -> 5) |x - 5|/(x - 5)`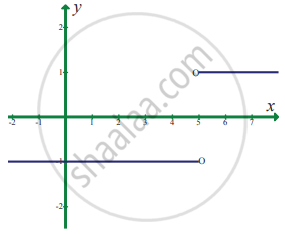
If the limit of f(x) as x approaches 2 is 4, can you conclude anything about f(2)? Explain reasoning
Evaluate the following limits:
`lim_(x ->) (x^"m" - 1)/(x^"n" - 1)`, m and n are integers
Evaluate the following limits:
`lim_(x -> 0) (sqrt(1 + x) - 1)/x`
Evaluate the following limits:
`lim_(x -> 1) (root(3)(7 + x^3) - sqrt(3 + x^2))/(x - 1)`
Evaluate the following limits:
`lim_(x -> 5) (sqrt(x - 1) - 2)/(x - 5)`
Evaluate the following limits:
`lim_(x -> 3) (x^2 - 9)/(x^2(x^2 - 6x + 9))`
Evaluate the following limits:
`lim_(x -> oo) (1 + x - 3x^3)/(1 + x^2 +3x^3)`
A tank contains 5000 litres of pure water. Brine (very salty water) that contains 30 grams of salt per litre of water is pumped into the tank at a rate of 25 litres per minute. The concentration of salt water after t minutes (in grams per litre) is C(t) = `(30"t")/(200 + "t")`. What happens to the concentration as t → ∞?
Evaluate the following limits:
`lim_(x -> 0) (sin("a" + x) - sin("a" - x))/x`
Choose the correct alternative:
`lim_(x -> oo) sinx/x`
Choose the correct alternative:
If `f(x) = x(- 1)^([1/x])`, x ≤ 0, then the value of `lim_(x -> 0) f(x)` is equal to
Choose the correct alternative:
`lim_(x -> 0) (x"e"^x - sin x)/x` is
