Advertisements
Advertisements
Question
Evaluate the following limits:
`lim_(x -> 0) (sqrt(2) - sqrt(1 + cosx))/(sin^2x)`
Solution
`lim_(x -> 0) ((sqrt(2) - sqrt(1 + cosx))/(sin^2x))`
= `lim_(x -> 0) ((sqrt(2) - sqrt(1 + cosx))(sqrt(2) + sqrt(1 + cosx)))/(sin^2x (sqrt(2) + sqrt(1 + cosx))`
= `lim_(x -> 0) (2 - (1 + cosx))/((1 - cos^2x)(sqrt(2) + sqrt(1 + cosx))`
= `lim_(x -> 0) (1 - cosx)/((1 +cosx)(1 - cosx)(sqrt(2) + sqrt(1 + cosx))`
= `lim_(x -> 0) 1/((1 + cosx)(sqrt(2) + sqrt(1 + cosx))`
= `1/((1 + cos0)(sqrt(2) + sqrt(1 + 1))`
= `1/(2(sqrt(2) + sqrt(2))`
=`1/(2 xx 2sqrt(2))`
`lim_(x -> 0) (sqrt(2) - sqrt(1 + cosx))/(sin^2x) = 1/(4sqrt(2))`
APPEARS IN
RELATED QUESTIONS
Evaluate the following limit:
If `lim_(x -> 1)[(x^4 - 1)/(x - 1)]` = `lim_(x -> "a")[(x^3 - "a"^3)/(x - "a")]`, find all possible values of a
Evaluate the following :
Given that 7x ≤ f(x) ≤ 3x2 – 6 for all x. Determine the value of `lim_(x -> 3) "f"(x)`
In exercise problems 7 – 15, use the graph to find the limits (if it exists). If the limit does not exist, explain why?
`lim_(x -> 3) (4 - x)`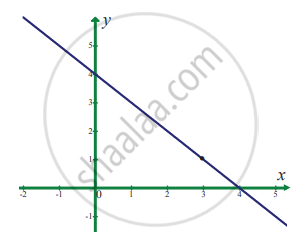
In exercise problems 7 – 15, use the graph to find the limits (if it exists). If the limit does not exist, explain why?
`lim_(x -> 5) |x - 5|/(x - 5)`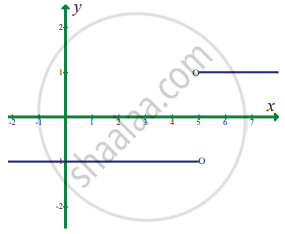
Sketch the graph of f, then identify the values of x0 for which `lim_(x -> x_0)` f(x) exists.
f(x) = `{{:(x^2",", x ≤ 2),(8 - 2x",", 2 < x < 4),(4",", x ≥ 4):}`
Sketch the graph of a function f that satisfies the given value:
f(0) is undefined
`lim_(x -> 0) f(x)` = 4
f(2) = 6
`lim_(x -> 2) f(x)` = 3
Evaluate : `lim_(x -> 3) (x^2 - 9)/(x - 3)` if it exists by finding `f(3^-)` and `f(3^+)`
Verify the existence of `lim_(x -> 1) f(x)`, where `f(x) = {{:((|x - 1|)/(x - 1)",", "for" x ≠ 1),(0",", "for" x = 1):}`
Evaluate the following limits:
`lim_(sqrt(x) -> 3) (x^2 - 81)/(sqrt(x) - 3)`
Evaluate the following limits:
`lim_(x -> 5) (sqrt(x - 1) - 2)/(x - 5)`
Evaluate the following limits:
`lim_(x -> oo) 3/(x - 2) - (2x + 11)/(x^2 + x - 6)`
Show that `lim_("n" -> oo) (1^2 + 2^2 + ... + (3"n")^2)/((1 + 2 + ... + 5"n")(2"n" + 3)) = 9/25`
Evaluate the following limits:
`lim_(x -> oo) ((x^2 - 2x + 1)/(x^2 -4x + 2))^x`
Evaluate the following limits:
`lim_(x -> 0) ("e"^x - "e"^(-x))/sinx`
Evaluate the following limits:
`lim_(x -> ) (sinx(1 - cosx))/x^3`
Choose the correct alternative:
`lim_(x -> 0) ("e"^(sin x) - 1)/x` =
Choose the correct alternative:
`lim_(x -> 0) ("e"^tanx - "e"^x)/(tan x - x)` =
If `lim_(x->1)(x^5-1)/(x-1)=lim_(x->k)(x^4-k^4)/(x^3-k^3),` then k = ______.
If `lim_(x -> 1) (x + x^2 + x^3|+ .... + x^n - n)/(x - 1)` = 820, (n ∈ N) then the value of n is equal to ______.
The value of `lim_(x→0)(sin(ℓn e^x))^2/((e^(tan^2x) - 1))` is ______.
