Advertisements
Online Mock Tests
Chapters
2: Basic Algebra
3: Trigonometry
4: Combinatorics and Mathematical Induction
5: Binomial Theorem, Sequences and Series
6: Two Dimensional Analytical Geometry
7: Matrices and Determinants
8: Vector Algebra
▶ 9: Differential Calculus - Limits and Continuity
10: Differential Calculus - Differentiability and Methods of Differentiation
11: Integral Calculus
12: Introduction to probability theory
![Samacheer Kalvi solutions for Mathematics - Volume 1 and 2 [English] Class 11 TN Board chapter 9 - Differential Calculus - Limits and Continuity Samacheer Kalvi solutions for Mathematics - Volume 1 and 2 [English] Class 11 TN Board chapter 9 - Differential Calculus - Limits and Continuity - Shaalaa.com](/images/mathematics-volume-1-and-2-english-class-11-tn-board_6:5f2b1b2038084cf381bfa42c826a928c.jpg)
Advertisements
Solutions for Chapter 9: Differential Calculus - Limits and Continuity
Below listed, you can find solutions for Chapter 9 of Tamil Nadu Board of Secondary Education Samacheer Kalvi for Mathematics - Volume 1 and 2 [English] Class 11 TN Board.
Samacheer Kalvi solutions for Mathematics - Volume 1 and 2 [English] Class 11 TN Board 9 Differential Calculus - Limits and Continuity Exercise 9.1 [Pages 95 - 98]
In problems 1 – 6, using the table estimate the value of the limit.
`lim_(x -> 2) (x - 2)/(x^2 - x - 2)`
| x | 1.9 | 1.99 | 1.999 | 2.001 | 2.01 | 2.1 |
| f(x) | 0.344820 | 0.33444 | 0.33344 | 0.333222 | 0.33222 | 0.332258 |
In problems 1 – 6, using the table estimate the value of the limit
`lim_(x -> 2) (x - 2)/(x^2 - 4)`
| x | 1.9 | 1.99 | 1.999 | 2.001 | 2.01 | 2.1 |
| f(x) | 0.25641 | 0.25062 | 0.250062 | 0.24993 | 0.24937 | 0.24390 |
In problems 1 – 6, using the table estimate the value of the limit
`lim_(x -> 0) (sqrt(x + 3) - sqrt(3))/x`
| x | – 0.1 | – 0.01 | – 0.001 | 0.001 | 0.01 | 0.1 |
| f(x) | 0.2911 | 0.2891 | 0.2886 | 0.2886 | 0.2885 | 0.28631 |
In problems 1 – 6, using the table estimate the value of the limit
`lim_(x -> - 3) (sqrt(1 - x) - 2)/(x + 3)`
| x | – 3.1 | – 3.01 | – 3.00 | – 2.999 | – 2.99 | – 2.9 |
| f(x) | – 0.24845 | – 0.24984 | – 0.24998 | – 0.25001 | – 0.25015 | – 0.25158 |
In problems 1 – 6, using the table estimate the value of the limit
`lim_(x -> 0) sin x/x`
| x | – 0.1 | – 0.01 | – 0.001 | 0.001 | 0.01 | 0.1 |
| f(x) | 0.99833 | 0.99998 | 0.99999 | 0.99999 | 0.99998 | 0.99833 |
In problems 1 – 6, using the table estimate the value of the limit
`lim_(x -> 0) (cos x - 1)/x`
| x | – 0.1 | – 0.01 | – 0.001 | 0.0001 | 0.01 | 0.1 |
| f(x) | 0.04995 | 0.0049999 | 0.0004999 | – 0.0004999 | – 0.004999 | – 0.04995 |
In exercise problems 7 – 15, use the graph to find the limits (if it exists). If the limit does not exist, explain why?
`lim_(x -> 3) (4 - x)`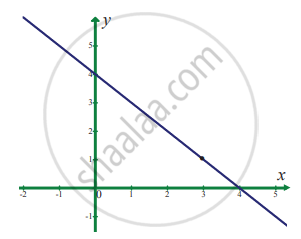
In exercise problems 7 – 15, use the graph to find the limits (if it exists). If the limit does not exist, explain why?
`lim_(x -> 1) (x^2 + 2)`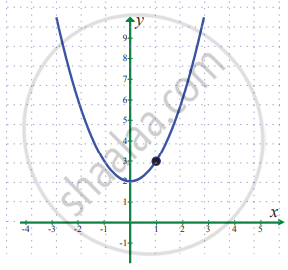
In exercise problems 7 – 15, use the graph to find the limits (if it exists). If the limit does not exist, explain why?
`lim_(x -> 2) f(x)` where `f(x) = {{:(4 - x",", x ≠ 2),(0",", x = 2):}`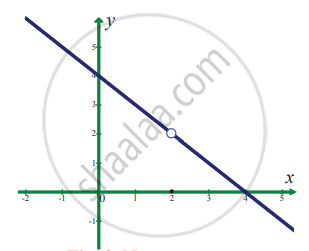
In exercise problems 7 – 15, use the graph to find the limits (if it exists). If the limit does not exist, explain why?
`lim_(x -> 1) f(x)` where `f(x) = {{:(x^2 + 2",", x ≠ 1),(1",", x = 1):}`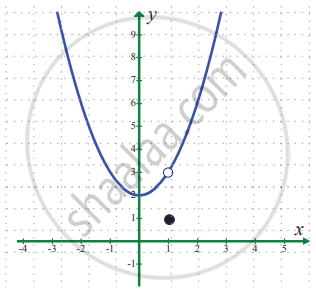
In exercise problems 7 – 15, use the graph to find the limits (if it exists). If the limit does not exist, explain why?
`lim_(x -> 3) 1/(x - 3)`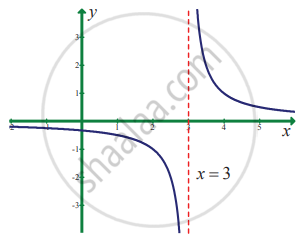
In exercise problems 7 – 15, use the graph to find the limits (if it exists). If the limit does not exist, explain why?
`lim_(x -> 5) |x - 5|/(x - 5)`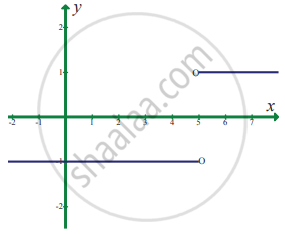
In exercise problems 7 – 15, use the graph to find the limits (if it exists). If the limit does not exist, explain why?
`lim_(x -> 1) sin pi x`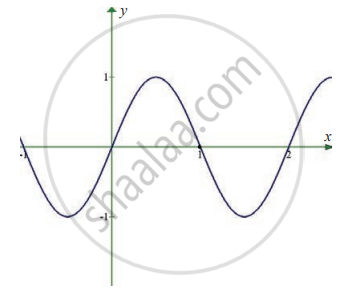
In exercise problems 7 – 15, use the graph to find the limits (if it exists). If the limit does not exist, explain why?
`lim_(x -> 0) sec x`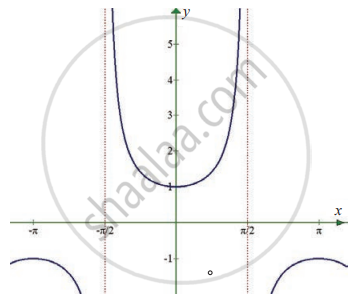
In exercise problems 7 – 15, use the graph to find the limits (if it exists). If the limit does not exist, explain why?
`lim_(x -> x/2) tan x`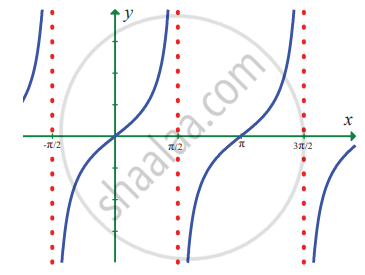
Sketch the graph of f, then identify the values of x0 for which `lim_(x -> x_0)` f(x) exists.
f(x) = `{{:(x^2",", x ≤ 2),(8 - 2x",", 2 < x < 4),(4",", x ≥ 4):}`
Sketch the graph of f, then identify the values of x0 for which `lim_(x -> x_0)` f(x) exists.
f(x) = `{{:(sin x",", x < 0),(1 - cos x",", 0 ≤ x ≤ pi),(cos x",", x > pi):}`
Sketch the graph of a function f that satisfies the given value:
f(0) is undefined
`lim_(x -> 0) f(x)` = 4
f(2) = 6
`lim_(x -> 2) f(x)` = 3
Sketch the graph of a function f that satisfies the given value:
f(– 2) = 0
f(2) = 0
`lim_(x -> 2) f(x)` = 0
`lim_(x -> 2) f(x)` does not exist.
Write a brief description of the meaning of the notation `lim_(x -> 8) f(x)` = 25
If f(2) = 4, can you conclude anything about the limit of f(x) as x approaches 2?
If the limit of f(x) as x approaches 2 is 4, can you conclude anything about f(2)? Explain reasoning
Evaluate : `lim_(x -> 3) (x^2 - 9)/(x - 3)` if it exists by finding `f(3^-)` and `f(3^+)`
Verify the existence of `lim_(x -> 1) f(x)`, where `f(x) = {{:((|x - 1|)/(x - 1)",", "for" x ≠ 1),(0",", "for" x = 1):}`
Samacheer Kalvi solutions for Mathematics - Volume 1 and 2 [English] Class 11 TN Board 9 Differential Calculus - Limits and Continuity Exercise 9.2 [Pages 102 - 103]
Evaluate the following limits:
`lim_(x -> 2) (x^4 - 16)/(x - 2)`
Evaluate the following limits:
`lim_(x ->) (x^"m" - 1)/(x^"n" - 1)`, m and n are integers
Evaluate the following limits:
`lim_(sqrt(x) -> 3) (x^2 - 81)/(sqrt(x) - 3)`
Evaluate the following limits:
`lim_("h" -> 0) (sqrt(x + "h") - sqrt(x))/"h", x > 0`
Evaluate the following limits:
`lim_(x -> 5) (sqrt(x + 4) - 3)/(x - 5)`
Evaluate the following limits:
`lim_(x -> 2) (1/x - 1/2)/(x - 2)`
Evaluate the following limits:
`lim_(x -> 1) (sqrt(x) - x^2)/(1 - sqrt(x))`
Evaluate the following limits:
`lim_(x -> 0) (sqrt(x^2 + 1) - 1)/(sqrt(x^2 + 16) - 4)`
Evaluate the following limits:
`lim_(x -> 0) (sqrt(1 + x) - 1)/x`
Evaluate the following limits:
`lim_(x -> 1) (root(3)(7 + x^3) - sqrt(3 + x^2))/(x - 1)`
Evaluate the following limits:
`lim_(x -> 2) (2 - sqrt(x + 2))/(root(3)(2) - root(3)(4 - x))`
Evaluate the following limits:
`lim_(x - 0) (sqrt(1 + x^2) - 1)/x`
Evaluate the following limits:
`lim_(x -> 0) (sqrt(1 - x) - 1)/x^2`
Evaluate the following limits:
`lim_(x -> 5) (sqrt(x - 1) - 2)/(x - 5)`
Evaluate the following limits:
`lim_(x -> "a") (sqrt(x - "b") - sqrt("a" - "b"))/(x^2 - "a"^2) ("a" > "b")`
Samacheer Kalvi solutions for Mathematics - Volume 1 and 2 [English] Class 11 TN Board 9 Differential Calculus - Limits and Continuity Exercise 9.3 [Page 111]
Find the left and right limits of f(x) = `(x^2 - 4)/((x^2 + 4x+ 4)(x + 3))` at x = – 2
Find the left and right limits of f(x) = tan x at x = `pi/2`
Evaluate the following limits:
`lim_(x -> 3) (x^2 - 9)/(x^2(x^2 - 6x + 9))`
Evaluate the following limits:
`lim_(x -> oo) 3/(x - 2) - (2x + 11)/(x^2 + x - 6)`
Evaluate the following limits:
`lim_(x -> oo) (x^3 + x)/(x^4 - 3x^2 + 1)`
Evaluate the following limits:
`lim_(x -> oo) (x^4 - 5x)/(x^2 - 3x + 1)`
Evaluate the following limits:
`lim_(x -> oo) (1 + x - 3x^3)/(1 + x^2 +3x^3)`
Evaluate the following limits:
`lim_(x ->oo) (x^3/(2x^2 - 1) - x^2/(2x + 1))`
Show that `lim_("n" -> oo) (1 + 2 + 3 + ... + "n")/(3"n"^2 + 7n" + 2) = 1/6`
Show that `lim_("n" -> oo) (1^2 + 2^2 + ... + (3"n")^2)/((1 + 2 + ... + 5"n")(2"n" + 3)) = 9/25`
Show that `lim_("n" -> oo) 1/1.2 + 1/2.3 + 1/3.4 + ... + 1/("n"("n" + 1))` = 1
An important problem in fishery science is to estimate the number of fish presently spawning in streams and use this information to predict the number of mature fish or “recruits” that will return to the rivers during the reproductive period. If S is the number of spawners and R the number of recruits, “Beverton-Holt spawner recruit function” is R(S) = `"S"/((alpha"S" + beta)` where `alpha` and `beta` are positive constants. Show that this function predicts approximately constant recruitment when the number of spawners is sufficiently large
A tank contains 5000 litres of pure water. Brine (very salty water) that contains 30 grams of salt per litre of water is pumped into the tank at a rate of 25 litres per minute. The concentration of salt water after t minutes (in grams per litre) is C(t) = `(30"t")/(200 + "t")`. What happens to the concentration as t → ∞?
Samacheer Kalvi solutions for Mathematics - Volume 1 and 2 [English] Class 11 TN Board 9 Differential Calculus - Limits and Continuity Exercise 9.4 [Pages 117 - 118]
Evaluate the following limits:
`lim_(x -> oo)(1 + 1/x)^(7x)`
Evaluate the following limits:
`lim_(x -> 0)(1 + x)^(1/(3x))`
Evaluate the following limits:
`lim_(x -> oo)(1 + "k"/x)^("m"/x)`
Evaluate the following limits:
`lim_(x -> oo) ((2x^2 + 3)/(2x^2 + 5))^(8x^2 + 3)`
Evaluate the following limits:
`lim_(x -> oo) (1 + 3/x)^(x + 2)`
Evaluate the following limits:
`lim_(x -> 0) (sin^3(x/2))/x^2`
Evaluate the following limits:
`lim_(x -> 0) (sinalphax)/(sinbetax)`
Evaluate the following limits:
`lim_(x -> 0) (tan 2x)/(sin 5x)`
Evaluate the following limits:
`lim_(alpha -> 0) (sin(alpha^"n"))/(sin alpha)^"m"`
Evaluate the following limits:
`lim_(x -> 0) (sin("a" + x) - sin("a" - x))/x`
Evaluate the following limits:
`lim_(x -> 0) (sqrt(x^2 + "a"^2) - "a")/(sqrt(x^2 + "b"^2) - "b")`
Evaluate the following limits:
`lim_(x -> 0) (2 "arc"sinx)/(3x)`
Evaluate the following limits:
`lim_(x-> 0) (1 - cos x)/x^2`
Evaluate the following limits:
`lim_(x -> 0) (tan 2x)/x`
Evaluate the following limits:
`lim_(x -> 0) (2^x - 3^x)/x`
Evaluate the following limits:
`lim_(x -> 0) (3^x - 1)/(sqrt(x + 1) - 1)`
Evaluate the following limits:
`lim_(x -> 0) (1 - cos^2x)/(x sin2x)`
Evaluate the following limits:
`lim_(x -> oo) x [3^(1/x) + 1 - cos(1/x) - "e"^(1/x)]`
Evaluate the following limits:
`lim_(x - oo){x[log(x + "a") - log(x)]}`
Evaluate the following limits:
`lim_(x -> pi) (sin3x)/(sin2x)`
Evaluate the following limits:
`lim_(x -> pi) (1 + sinx)^(2"cosec"x)`
Evaluate the following limits:
`lim_(x -> 0) (sqrt(2) - sqrt(1 + cosx))/(sin^2x)`
Evaluate the following limits:
`lim_(x -> 0) (sqrt(1 + sinx) - sqrt(1 - sinx))/tanx`
Evaluate the following limits:
`lim_(x -> oo) ((x^2 - 2x + 1)/(x^2 -4x + 2))^x`
Evaluate the following limits:
`lim_(x -> 0) ("e"^x - "e"^(-x))/sinx`
Evaluate the following limits:
`lim_(x -> 0) ("e"^("a"x) - "e"^("b"x))/x`
Evaluate the following limits:
`lim_(x -> ) (sinx(1 - cosx))/x^3`
Evaluate the following limits:
`lim_(x -> 0) (tan x - sin x)/x^3`
Samacheer Kalvi solutions for Mathematics - Volume 1 and 2 [English] Class 11 TN Board 9 Differential Calculus - Limits and Continuity Exercise 9.5 [Pages 127 - 129]
Prove that f(x) = 2x2 + 3x - 5 is continuous at all points in R
Examine the continuity of the following:
x + sin x
Examine the continuity of the following:
x2 cos x
Examine the continuity of the following:
ex tan x
Examine the continuity of the following:
e2x + x2
Examine the continuity of the following:
x . log x
Examine the continuity of the following:
`sinx/x^2`
Examine the continuity of the following:
`(x^2 - 16)/(x + 4)`
Examine the continuity of the following:
|x + 2| + |x – 1|
Examine the continuity of the following:
`|x - 2|/|x + 1|`
Examine the continuity of the following:
cot x + tan x
Find the points of discontinuity of the function f, where `f(x) = {{:(4x + 5",", "if", x ≤ 3),(4x - 5",", "if", x > 3):}`
Find the points of discontinuity of the function f, where `f(x) = {{:(x + 2",", "if", x ≥ 2),(x^2",", "if", x < 2):}`
Find the points of discontinuity of the function f, where `f(x) = {{:(x^3 - 3",", "if" x ≤ 2),(x^2 + 1",", "if" x < 2):}`
Find the points of discontinuity of the function f, where `f(x) = {{:(sinx",", 0 ≤ x ≤ pi/4),(cos x",", pi/4 < x < pi/2):}`
At the given point x0 discover whether the given function is continuous or discontinuous citing the reasons for your answer:
x0 = 1, `f(x) = {{:((x^2 - 1)/(x - 1)",", x ≠ 1),(2",", x = 1):}`
At the given point x0 discover whether the given function is continuous or discontinuous citing the reasons for your answer:
x0 = 3, `f(x) = {{:((x^2 - 9)/(x - 3)",", "if" x ≠ 3),(5",", "if" x = 3):}`
Show that the function `{{:((x^3 - 1)/(x - 1)",", "if" x ≠ 1),(3",", "if" x = 1):}` is continuous om `(- oo, oo)`
For what value of `alpha` is this function `f(x) = {{:((x^4 - 1)/(x - 1)",", "if" x ≠ 1),(alpha",", "if" x = 1):}` continuous at x = 1?
Let `f(x) = {{:(0",", "if" x < 0),(x^2",", "if" 0 ≤ x ≤ 2),(4",", "if" x ≥ 2):}`. Graph the function. Show that f(x) continuous on `(- oo, oo)`
If f and g are continuous functions with f(3) = 5 and `lim_(x -> 3) [2f(x) - g(x)]` = 4, find g(3)
Find the points at which f is discontinuous. At which of these points f is continuous from the right, from the left, or neither? Sketch the graph of f.
`f(x) = {{:(2x + 1",", "if" x ≤ - 1),(3x",", "if" - 1 < x < 1),(2x - 1",", "if" x ≥ 1):}`
Find the points at which f is discontinuous. At which of these points f is continuous from the right, from the left, or neither? Sketch the graph of f.
`f(x) = {{:((x - 1)^3",", "if" x < 0),((x + 1)^3",", "if" x ≥ 0):}`
A function f is defined as follows:
`f(x) = {{:(0, "for" x < 0;),(x, "for" 0 ≤ x ≤ 1;),(- x^2 +4x - 2, "for" 1 ≤ x ≤ 3;),(4 - x, "for" x ≥ 3):}`
Is the function continuous?
Which of the following functions f has a removable discontinuity at x = x0? If the discontinuity is removable, find a function g that agrees with f for x ≠ x0 and is continuous on R.
`f(x) = (x^2 - 2x - 8)/(x + 2), x_0` = – 2
Which of the following functions f has a removable discontinuity at x = x0? If the discontinuity is removable, find a function g that agrees with f for x ≠ x0 and is continuous on R.
`f(x) = (x^3 + 64)/(x + 4), x_0` = – 4
Which of the following functions f has a removable discontinuity at x = x0? If the discontinuity is removable, find a function g that agrees with f for x ≠ x0 and is continuous on R.
`f(x) = (3 - sqrt(x))/(9 - x), x_0` = 9
Find the constant b that makes g continuous on `(- oo, oo)`.
`g(x) = {{:(x^2 - "b"^2,"if" x < 4),("b"x + 20, "if" x ≥ 4):}`
Consider the function `f(x) = x sin pi/x`. What value must we give f(0) in order to make the function continuous everywhere?
The function `f(x) = (x^2 - 1)/(x^3 - 1)` is not defined at x = 1. What value must we give f(1) inorder to make f(x) continuous at x =1?
State how continuity is destroyed at x = x0 for the following graphs.
State how continuity is destroyed at x = x0 for the following graphs.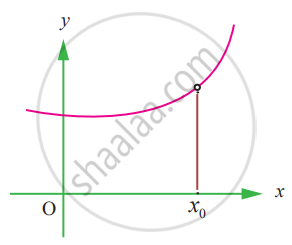
State how continuity is destroyed at x = x0 for the following graphs.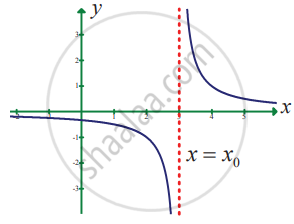
State how continuity is destroyed at x = x0 for the following graphs.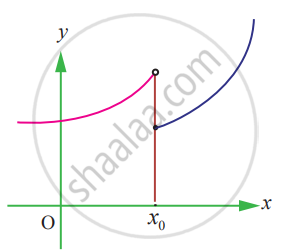
Samacheer Kalvi solutions for Mathematics - Volume 1 and 2 [English] Class 11 TN Board 9 Differential Calculus - Limits and Continuity Exercise 9.6 [Pages 129 - 131]
Choose the correct alternative:
`lim_(x -> oo) sinx/x`
1
0
`oo`
`- oo`
Choose the correct alternative:
`lim_(x - pi/2) (2x - pi)/cos x`
2
1
−2
0
Choose the correct alternative:
`lim_(x -> 0) sqrt(1 - cos 2x)/x`
0
1
`sqrt(2)`
does not exist
Choose the correct alternative:
`lim_(theta -> 0) (sinsqrt(theta))/(sqrt(sin theta)`
1
– 1
0
2
Choose the correct alternative:
`lim_(x -> oo) ((x^2 + 5x + 3)/(x^2 + x + 3))^x` is
e4
e2
e3
1
Choose the correct alternative:
`lim_(x - oo) sqrt(x^2 - 1)/(2x + 1)` =
1
0
– 1
`1/2`
Choose the correct alternative:
`lim_(x -> 0) ("a"^x - "b"^x)/x` =
log ab
`log ("a"/"b")`
`log ("b"/"a")`
`"a"/"b"`
Choose the correct alternative:
`lim_(x -> 0) (8^x - 4x - 2^x + 1^x)/x^2` =
2 log 2
2(log)2
log 2
3 log 2
Choose the correct alternative:
If `f(x) = x(- 1)^([1/x])`, x ≤ 0, then the value of `lim_(x -> 0) f(x)` is equal to
– 1
0
2
4
Choose the correct alternative:
`lim_(x -> 3) [x]` =
2
3
does not exist
0
Choose the correct alternative:
Let the function f be defined by `f(x) = {{:(3x, 0 ≤ x ≤ 1),(-3 + 5, 1 < x ≤ 2):}`, then
`lim_(x -> 1) f(x)` = 1
`lim_(x -> 1) f(x)` = 3
`lim_(x -> 1) f(x)` = 2
`lim_(x -> 1) f(x)` does not exist
Choose the correct alternative:
If f : R → R is defined by `f(x) = [x - 3] + |x - 4|` for x ∈ R then `lim_(x -> 3^-) f(x)` is equal to
– 2
– 1
0
1
Choose the correct alternative:
`lim_(x -> 0) (x"e"^x - sin x)/x` is
1
2
3
0
Choose the correct alternative:
If `lim_(x -> 0) (sin "p"x)/(tan 3x)` = 4, then the value of p is
6
9
12
4
Choose the correct alternative:
`lim_(alpha - pi/4) (sin alpha - cos alpha)/(alpha - pi/4)` is
`sqrt(2)`
`1/sqrt(2)`
1
2
Choose the correct alternative:
`lim_(x -> oo) (1/"n"^2 + 2/"n"^2 + 3/"n"^2 + ... + "n"/"n"^2)` is
`1/2`
0
1
`oo`
Choose the correct alternative:
`lim_(x -> 0) ("e"^(sin x) - 1)/x` =
1
e
`1/"e"`
0
Choose the correct alternative:
`lim_(x -> 0) ("e"^tanx - "e"^x)/(tan x - x)` =
1
e
`1/2`
0
Choose the correct alternative:
The value of `lim_(x -> 0) sinx/sqrt(x^2)` is
1
– 1
0
limit does not exist
Choose the correct alternative:
The value of `lim_(x -> "k") x - [x]`, where k is an integer is
– 1
1
0
2
Choose the correct alternative:
At x = `3/2` the function f(x) = `|2x - 3|/(2x - 3)` is
Continuous
Discontinuous
Differentiable
Non-zero
Choose the correct alternative:
Let f : R → R be defined by `f(x) = {{:(x, x "is irrational"),(1 - x, x "is rational"):}` then f is
Discontinuous at x = `1/2`
Continuous at x = `1/2`
Continuous everywhere
Discontinuous everywhere
Choose the correct alternative:
The function `f(x) = {{:((x^2 - 1)/(x^3 + 1), x ≠ - 1),("P", x = -1):}` is not defined for x = −1. The value of f(−1) so that the function extended by this value is continuous is
`2/3`
`- 2/3`
1
0
Choose the correct alternative:
Let f be a continuous function on [2, 5]. If f takes only rational values for all x and f(3) = 12, then f(4.5) is equal to
`(f(3) + f(4.5))/7.5`
12
17.5
`(f(4.5) - f(3))/1.5`
Choose the correct alternative:
Let a function f be defined by `f(x) = (x - |x|)/x` for x ≠ 0 and f(0) = 2. Then f is
Continuous nowhere
Continuous everywhere
Continuous for all x except x = 1
Continuous for all x except x = 0
Solutions for 9: Differential Calculus - Limits and Continuity
![Samacheer Kalvi solutions for Mathematics - Volume 1 and 2 [English] Class 11 TN Board chapter 9 - Differential Calculus - Limits and Continuity Samacheer Kalvi solutions for Mathematics - Volume 1 and 2 [English] Class 11 TN Board chapter 9 - Differential Calculus - Limits and Continuity - Shaalaa.com](/images/mathematics-volume-1-and-2-english-class-11-tn-board_6:5f2b1b2038084cf381bfa42c826a928c.jpg)
Samacheer Kalvi solutions for Mathematics - Volume 1 and 2 [English] Class 11 TN Board chapter 9 - Differential Calculus - Limits and Continuity
Shaalaa.com has the Tamil Nadu Board of Secondary Education Mathematics Mathematics - Volume 1 and 2 [English] Class 11 TN Board Tamil Nadu Board of Secondary Education solutions in a manner that help students grasp basic concepts better and faster. The detailed, step-by-step solutions will help you understand the concepts better and clarify any confusion. Samacheer Kalvi solutions for Mathematics Mathematics - Volume 1 and 2 [English] Class 11 TN Board Tamil Nadu Board of Secondary Education 9 (Differential Calculus - Limits and Continuity) include all questions with answers and detailed explanations. This will clear students' doubts about questions and improve their application skills while preparing for board exams.
Further, we at Shaalaa.com provide such solutions so students can prepare for written exams. Samacheer Kalvi textbook solutions can be a core help for self-study and provide excellent self-help guidance for students.
Concepts covered in Mathematics - Volume 1 and 2 [English] Class 11 TN Board chapter 9 Differential Calculus - Limits and Continuity are Introduction to Differential Calculus -limits and Continuity, Continuity, Concept of Limits.
Using Samacheer Kalvi Mathematics - Volume 1 and 2 [English] Class 11 TN Board solutions Differential Calculus - Limits and Continuity exercise by students is an easy way to prepare for the exams, as they involve solutions arranged chapter-wise and also page-wise. The questions involved in Samacheer Kalvi Solutions are essential questions that can be asked in the final exam. Maximum Tamil Nadu Board of Secondary Education Mathematics - Volume 1 and 2 [English] Class 11 TN Board students prefer Samacheer Kalvi Textbook Solutions to score more in exams.
Get the free view of Chapter 9, Differential Calculus - Limits and Continuity Mathematics - Volume 1 and 2 [English] Class 11 TN Board additional questions for Mathematics Mathematics - Volume 1 and 2 [English] Class 11 TN Board Tamil Nadu Board of Secondary Education, and you can use Shaalaa.com to keep it handy for your exam preparation.
