Advertisements
Advertisements
Question
Evaluate the following limits:
`lim_(x -> 0) (sqrt(x^2 + "a"^2) - "a")/(sqrt(x^2 + "b"^2) - "b")`
Solution
We know `lim_(x -> "a") (x^"n" - "a"^"a")/(x -"a") = "na"^("n" - 1)`
`lim_(x -> 0)((sqrt((x^2 + "a"^2)) - "a")/(sqrt((x^2 + "b"^2)) - "b")) = lim_(x -> 0)(((x^2 + "a"^2)^(1/2) - ("a"^2)^(1/2))/((x^2 + "b"^2)^(1/2) - ("b"^2)^(1/2)))`
= `lim_(x -> 0) ((x^2 + "a"^2)^(1/2) - ("a"^2)^(1/2))/x^2 xx x^2/((x^2 + "b"^2)^(1/2) - ("b"^2)^(1/2))`
= `lim_(x -> 0) ((x^2 + "a"^2)^(1/2) - ("a"^2)^(1/2))/((x^2 + "a"^2) - "a"^2) xx ((x^2 + "b"^2) - "b"^2)/((x^2 + "b"^2)^(1/2) - ("b"^2)^(1/2))`
= `lim_(x -> 0) ((x^2 + "a"^2)^(1/2) - ("a"^2)^(1/2))/((x^2 + "a"^2) - "a"^2) xx lim_(x -> 0) 1/(((x^2 + "b"^2)^(1/2) - ("b"^2)^(1/2))/((x^2 + "b"^2) - "b"^2)`
Put x2 + a2 = y
Put x2 + b2 = z
When x = 0
⇒ y = a2
When x = 0
⇒ z = b2
= `lim_(y -> "a"^2)((y^(1/2) - ("a"^2)^(1/))/(y - "a"^2)) xx 1/(lim_(x -> "b"^2)(("z"^(1/2) - ("b"^2)^(1/2))/("z" - "b"^2))`
= `1/2 ("a"^2)^(1/2 - 1) xx 1/(1/2 ("b"^2)^(1/2 - 1))`
= `(("a"^2)^(- 1/2))/(("b"^2)^(- 1/2))`
= `("a"^(- 1))/("b"^(- 1))`
= `"b"/"a"`
`lim_(x -> 0)((sqrt((x^2 + "a"^2)) - "a")/(sqrt((x^2 + "b"^2)) - "b")) = "b"/"a"`
APPEARS IN
RELATED QUESTIONS
Evaluate the following limit:
`lim_(y -> -3) [(y^5 + 243)/(y^3 + 27)]`
Evaluate the following limit:
`lim_(x -> 3)[sqrt(2x + 6)/x]`
Evaluate the following limit :
`lim_(x -> 1)[(x + x^2 + x^3 + ......... + x^"n" - "n")/(x - 1)]`
Evaluate the following :
`lim_(x -> 0)[x/(|x| + x^2)]`
In exercise problems 7 – 15, use the graph to find the limits (if it exists). If the limit does not exist, explain why?
`lim_(x -> x/2) tan x`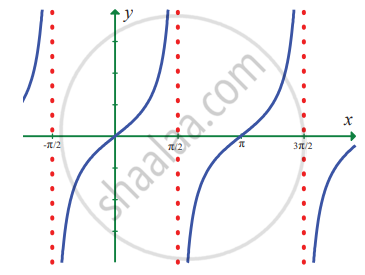
Verify the existence of `lim_(x -> 1) f(x)`, where `f(x) = {{:((|x - 1|)/(x - 1)",", "for" x ≠ 1),(0",", "for" x = 1):}`
Evaluate the following limits:
`lim_(x ->) (x^"m" - 1)/(x^"n" - 1)`, m and n are integers
Evaluate the following limits:
`lim_(x -> 1) (sqrt(x) - x^2)/(1 - sqrt(x))`
Evaluate the following limits:
`lim_(x -> 0) (sqrt(1 - x) - 1)/x^2`
Find the left and right limits of f(x) = tan x at x = `pi/2`
A tank contains 5000 litres of pure water. Brine (very salty water) that contains 30 grams of salt per litre of water is pumped into the tank at a rate of 25 litres per minute. The concentration of salt water after t minutes (in grams per litre) is C(t) = `(30"t")/(200 + "t")`. What happens to the concentration as t → ∞?
Evaluate the following limits:
`lim_(x -> oo) (1 + 3/x)^(x + 2)`
Evaluate the following limits:
`lim_(x -> 0) (sin("a" + x) - sin("a" - x))/x`
Evaluate the following limits:
`lim_(x-> 0) (1 - cos x)/x^2`
Evaluate the following limits:
`lim_(x -> pi) (1 + sinx)^(2"cosec"x)`
Choose the correct alternative:
`lim_(x -> 0) ("e"^(sin x) - 1)/x` =
`lim_(x→0^+)(int_0^(x^2)(sinsqrt("t"))"dt")/x^3` is equal to ______.
`lim_(x→-1) (x^3 - 2x - 1)/(x^5 - 2x - 1)` = ______.
`lim_(x→∞)((x + 7)/(x + 2))^(x + 4)` is ______.
