Advertisements
Advertisements
Question
Evaluate the following :
Solution
We know that |x| = x if x > 0
= – x if x < 0
∴
=
=
=
=
=
= 1
=
=
=
=
=
= – 1
∴
∴
APPEARS IN
RELATED QUESTIONS
Evaluate the following limit:
Evaluate the following limit :
Evaluate the following limit :
Evaluate the following limit :
Evaluate the following limit :
Evaluate the following :
In problems 1 – 6, using the table estimate the value of the limit
| x | 1.9 | 1.99 | 1.999 | 2.001 | 2.01 | 2.1 |
| f(x) | 0.25641 | 0.25062 | 0.250062 | 0.24993 | 0.24937 | 0.24390 |
In exercise problems 7 – 15, use the graph to find the limits (if it exists). If the limit does not exist, explain why?
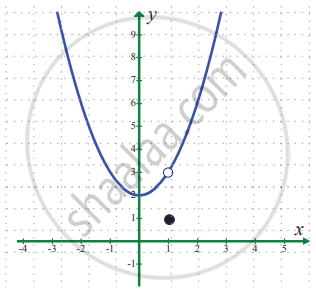
Sketch the graph of f, then identify the values of x0 for which
f(x) =
If f(2) = 4, can you conclude anything about the limit of f(x) as x approaches 2?
If the limit of f(x) as x approaches 2 is 4, can you conclude anything about f(2)? Explain reasoning
Evaluate the following limits:
Evaluate the following limits:
Evaluate the following limits:
Evaluate the following limits:
Show that
Evaluate the following limits:
Evaluate the following limits:
Evaluate the following limits:
Evaluate the following limits:
Evaluate the following limits:
Evaluate the following limits:
Evaluate the following limits:
Evaluate the following limits:
Evaluate the following limits:
Evaluate the following limits:
Evaluate the following limits:
Choose the correct alternative:
Choose the correct alternative:
Choose the correct alternative:
Choose the correct alternative:
Choose the correct alternative:
Choose the correct alternative:
