Advertisements
Advertisements
Question
Show that `lim_("n" -> oo) 1/1.2 + 1/2.3 + 1/3.4 + ... + 1/("n"("n" + 1))` = 1
Solution
Tn = `1/("n"("n" + 1))`
`1/("n"("n" + 1)) = "A"/"n" + "B"/("n" +1)`
1 = A(n + 1) + Bn
Put n = 0
1 = A(0 + 1) + B × 0
A = 1
Put n = – 1
1 = A(– 1 + 1) + B(– 1)
1 = 0 – B
⇒ B = – 1
`1/("n"("n" + 1)) = 1/"n" - 1/("n" + 1)`
Tn = `1/"n" - 1/("n" + 1)`
T1 = `1/1- 1/2`
T2 = `1/2 - 1/3`
T3 = `1/3 - 1/4`
........................
........................
Tn = `1/"n" - 1/("n" + 1)`
T1 + T2 + .... + Tn = `(1/1 - 1/2) + (1/2 - 1/3) + (1/3 - 1/4) + .... + (1/"n" - 1/("n" + 1))`
T1 + T2 + .... + Tn = `(1 - 1/("n" + 1))`
`lim_("n" -> oo) ("T"_1 + "T"_2 + .... + "T"_"n") = lim_("n" -> oo) (1 - 1/("n" + 1))`
= `1 - lim_("n" -> oo) 1/("n" + 1)`
= 1 – 0
`lim_("n" -> oo) 1/1.2 + 1/2.3 + 1/3.4 + ... + 1/("n"("n" + 1))` = 1
APPEARS IN
RELATED QUESTIONS
Evaluate the following limit :
If `lim_(x -> 5) [(x^"k" - 5^"k")/(x - 5)]` = 500, find all possible values of k.
In the following example, given ∈ > 0, find a δ > 0 such that whenever, |x – a| < δ, we must have |f(x) – l| < ∈.
`lim_(x -> 2)(2x + 3)` = 7
In exercise problems 7 – 15, use the graph to find the limits (if it exists). If the limit does not exist, explain why?
`lim_(x -> 2) f(x)` where `f(x) = {{:(4 - x",", x ≠ 2),(0",", x = 2):}`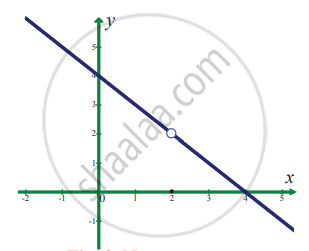
In exercise problems 7 – 15, use the graph to find the limits (if it exists). If the limit does not exist, explain why?
`lim_(x -> 5) |x - 5|/(x - 5)`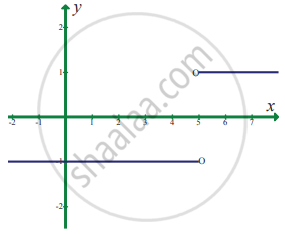
In exercise problems 7 – 15, use the graph to find the limits (if it exists). If the limit does not exist, explain why?
`lim_(x -> 0) sec x`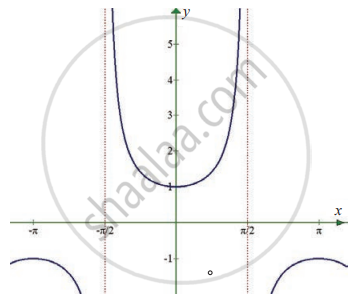
Sketch the graph of a function f that satisfies the given value:
f(– 2) = 0
f(2) = 0
`lim_(x -> 2) f(x)` = 0
`lim_(x -> 2) f(x)` does not exist.
Write a brief description of the meaning of the notation `lim_(x -> 8) f(x)` = 25
Evaluate the following limits:
`lim_(sqrt(x) -> 3) (x^2 - 81)/(sqrt(x) - 3)`
Evaluate the following limits:
`lim_(x -> 2) (2 - sqrt(x + 2))/(root(3)(2) - root(3)(4 - x))`
Evaluate the following limits:
`lim_(x -> 5) (sqrt(x - 1) - 2)/(x - 5)`
Evaluate the following limits:
`lim_(x -> 3) (x^2 - 9)/(x^2(x^2 - 6x + 9))`
Evaluate the following limits:
`lim_(x -> oo) 3/(x - 2) - (2x + 11)/(x^2 + x - 6)`
Evaluate the following limits:
`lim_(x -> 0) (sqrt(x^2 + "a"^2) - "a")/(sqrt(x^2 + "b"^2) - "b")`
Evaluate the following limits:
`lim_(x -> 0) (tan 2x)/x`
Evaluate the following limits:
`lim_(x -> 0) (sqrt(2) - sqrt(1 + cosx))/(sin^2x)`
Choose the correct alternative:
`lim_(x - pi/2) (2x - pi)/cos x`
Choose the correct alternative:
`lim_(x -> 0) ("e"^(sin x) - 1)/x` =
`lim_(x→∞)((x + 7)/(x + 2))^(x + 4)` is ______.
The value of `lim_(x→0)(sin(ℓn e^x))^2/((e^(tan^2x) - 1))` is ______.
