Advertisements
Advertisements
Question
In exercise problems 7 – 15, use the graph to find the limits (if it exists). If the limit does not exist, explain why?
`lim_(x -> 2) f(x)` where `f(x) = {{:(4 - x",", x ≠ 2),(0",", x = 2):}`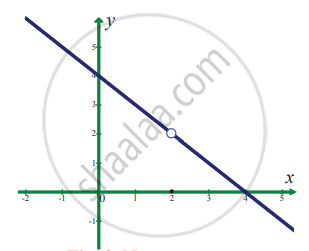
Solution
`f(x) = {{:(4 - x",", x ≠ 2),(0",", x = 2):}`
To find `lim_(x -> 2) f(x)`
From the figure the value of the function at x = 2 is y = f(2) = 2
∴ `lim_(x -> 2) f(x)` = 2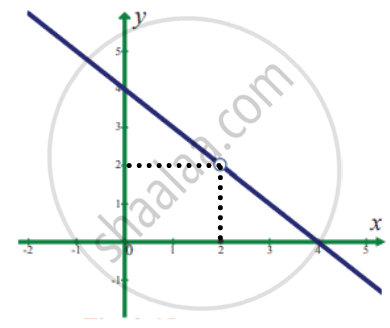
APPEARS IN
RELATED QUESTIONS
Evaluate the following limit:
`lim_(x -> 5)[(x^3 - 125)/(x^5 - 3125)]`
Evaluate the following limit :
`lim_(x -> 0)[((1 - x)^8 - 1)/((1 - x)^2 - 1)]`
Evaluate the following :
`lim_(x -> 0)[x/(|x| + x^2)]`
Evaluate the following :
`lim_(x -> 0) [(sqrt(1 - cosx))/x]`
In problems 1 – 6, using the table estimate the value of the limit
`lim_(x -> 0) sin x/x`
| x | – 0.1 | – 0.01 | – 0.001 | 0.001 | 0.01 | 0.1 |
| f(x) | 0.99833 | 0.99998 | 0.99999 | 0.99999 | 0.99998 | 0.99833 |
In exercise problems 7 – 15, use the graph to find the limits (if it exists). If the limit does not exist, explain why?
`lim_(x -> x/2) tan x`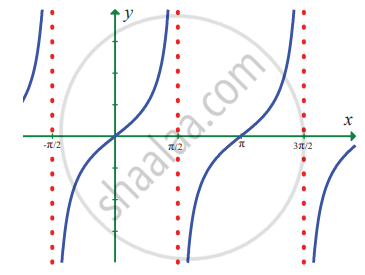
Sketch the graph of f, then identify the values of x0 for which `lim_(x -> x_0)` f(x) exists.
f(x) = `{{:(sin x",", x < 0),(1 - cos x",", 0 ≤ x ≤ pi),(cos x",", x > pi):}`
Write a brief description of the meaning of the notation `lim_(x -> 8) f(x)` = 25
Evaluate the following limits:
`lim_(x -> 2) (1/x - 1/2)/(x - 2)`
Evaluate the following limits:
`lim_(x -> 0) (sqrt(1 + x) - 1)/x`
Evaluate the following limits:
`lim_(x - 0) (sqrt(1 + x^2) - 1)/x`
Show that `lim_("n" -> oo) 1/1.2 + 1/2.3 + 1/3.4 + ... + 1/("n"("n" + 1))` = 1
Evaluate the following limits:
`lim_(x -> oo)(1 + 1/x)^(7x)`
Evaluate the following limits:
`lim_(x -> oo)(1 + "k"/x)^("m"/x)`
Evaluate the following limits:
`lim_(x -> 0) (3^x - 1)/(sqrt(x + 1) - 1)`
Evaluate the following limits:
`lim_(x -> pi) (1 + sinx)^(2"cosec"x)`
Evaluate the following limits:
`lim_(x -> 0) ("e"^("a"x) - "e"^("b"x))/x`
Choose the correct alternative:
`lim_(x -> 0) sqrt(1 - cos 2x)/x`
`lim_(x→-1) (x^3 - 2x - 1)/(x^5 - 2x - 1)` = ______.
