Advertisements
Advertisements
Question
In exercise problems 7 – 15, use the graph to find the limits (if it exists). If the limit does not exist, explain why?
`lim_(x -> 1) (x^2 + 2)`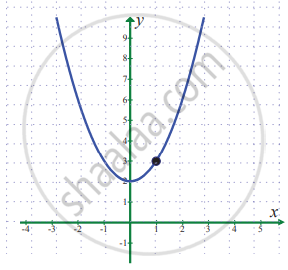
Solution
From the graph the value of the function at x = 1 is y = f(1) = 3
∴ `lim_(x -> 1) (x^2 + 2)` = 3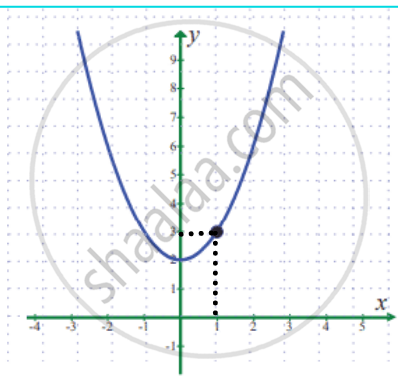
APPEARS IN
RELATED QUESTIONS
Evaluate the following limit:
`lim_(y -> -3) [(y^5 + 243)/(y^3 + 27)]`
Evaluate the following limit:
If `lim_(x -> 1)[(x^4 - 1)/(x - 1)]` = `lim_(x -> "a")[(x^3 - "a"^3)/(x - "a")]`, find all possible values of a
Evaluate the following limit :
If `lim_(x -> 5) [(x^"k" - 5^"k")/(x - 5)]` = 500, find all possible values of k.
Evaluate the following limit :
`lim_(z -> "a")[((z + 2)^(3/2) - ("a" + 2)^(3/2))/(z - "a")]`
In problems 1 – 6, using the table estimate the value of the limit
`lim_(x -> - 3) (sqrt(1 - x) - 2)/(x + 3)`
| x | – 3.1 | – 3.01 | – 3.00 | – 2.999 | – 2.99 | – 2.9 |
| f(x) | – 0.24845 | – 0.24984 | – 0.24998 | – 0.25001 | – 0.25015 | – 0.25158 |
Evaluate : `lim_(x -> 3) (x^2 - 9)/(x - 3)` if it exists by finding `f(3^-)` and `f(3^+)`
Evaluate the following limits:
`lim_(x -> 0) (sqrt(x^2 + 1) - 1)/(sqrt(x^2 + 16) - 4)`
Evaluate the following limits:
`lim_(x -> 0) (sqrt(1 + x) - 1)/x`
Evaluate the following limits:
`lim_(x - 0) (sqrt(1 + x^2) - 1)/x`
Find the left and right limits of f(x) = tan x at x = `pi/2`
Evaluate the following limits:
`lim_(x -> oo) (x^3 + x)/(x^4 - 3x^2 + 1)`
Evaluate the following limits:
`lim_(x -> 0)(1 + x)^(1/(3x))`
Evaluate the following limits:
`lim_(x -> 0) (tan 2x)/x`
Choose the correct alternative:
`lim_(x -> 0) ("a"^x - "b"^x)/x` =
If `lim_(x->1)(x^5-1)/(x-1)=lim_(x->k)(x^4-k^4)/(x^3-k^3),` then k = ______.
`lim_(x -> 0) (sin 4x + sin 2x)/(sin5x - sin3x)` = ______.
`lim_(x→0^+)(int_0^(x^2)(sinsqrt("t"))"dt")/x^3` is equal to ______.
`lim_(x→∞)((x + 7)/(x + 2))^(x + 4)` is ______.
