Advertisements
Advertisements
प्रश्न
In exercise problems 7 – 15, use the graph to find the limits (if it exists). If the limit does not exist, explain why?
`lim_(x -> 2) f(x)` where `f(x) = {{:(4 - x",", x ≠ 2),(0",", x = 2):}`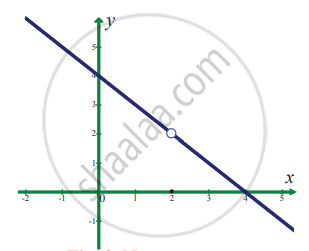
उत्तर
`f(x) = {{:(4 - x",", x ≠ 2),(0",", x = 2):}`
To find `lim_(x -> 2) f(x)`
From the figure the value of the function at x = 2 is y = f(2) = 2
∴ `lim_(x -> 2) f(x)` = 2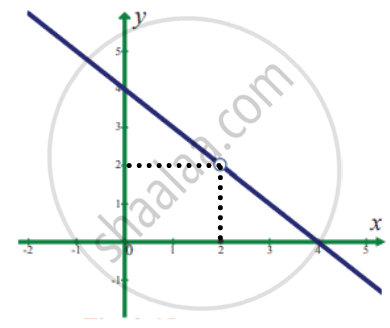
APPEARS IN
संबंधित प्रश्न
Evaluate the following :
`lim_(x -> 0)[x/(|x| + x^2)]`
Evaluate the following :
`lim_(x -> 0) [(sqrt(1 - cosx))/x]`
Evaluate the following :
`lim_(x -> 0) {1/x^12 [1 - cos(x^2/2) - cos(x^4/4) + cos(x^2/2) cos(x^4/4)]}`
In exercise problems 7 – 15, use the graph to find the limits (if it exists). If the limit does not exist, explain why?
`lim_(x -> 1) sin pi x`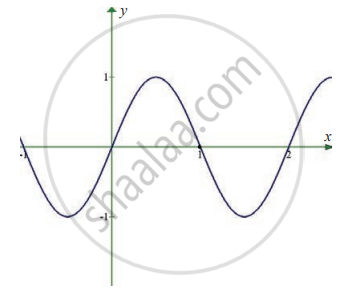
In exercise problems 7 – 15, use the graph to find the limits (if it exists). If the limit does not exist, explain why?
`lim_(x -> x/2) tan x`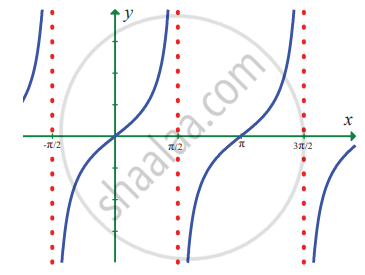
Sketch the graph of a function f that satisfies the given value:
f(0) is undefined
`lim_(x -> 0) f(x)` = 4
f(2) = 6
`lim_(x -> 2) f(x)` = 3
If the limit of f(x) as x approaches 2 is 4, can you conclude anything about f(2)? Explain reasoning
Evaluate : `lim_(x -> 3) (x^2 - 9)/(x - 3)` if it exists by finding `f(3^-)` and `f(3^+)`
Evaluate the following limits:
`lim_(sqrt(x) -> 3) (x^2 - 81)/(sqrt(x) - 3)`
Evaluate the following limits:
`lim_(x -> 5) (sqrt(x - 1) - 2)/(x - 5)`
Find the left and right limits of f(x) = tan x at x = `pi/2`
Evaluate the following limits:
`lim_(x -> 3) (x^2 - 9)/(x^2(x^2 - 6x + 9))`
Evaluate the following limits:
`lim_(x -> oo) 3/(x - 2) - (2x + 11)/(x^2 + x - 6)`
Evaluate the following limits:
`lim_(x -> oo) (x^3 + x)/(x^4 - 3x^2 + 1)`
Evaluate the following limits:
`lim_(x -> oo) ((2x^2 + 3)/(2x^2 + 5))^(8x^2 + 3)`
Evaluate the following limits:
`lim_(x -> 0) (sqrt(x^2 + "a"^2) - "a")/(sqrt(x^2 + "b"^2) - "b")`
Evaluate the following limits:
`lim_(x -> oo) ((x^2 - 2x + 1)/(x^2 -4x + 2))^x`
Evaluate the following limits:
`lim_(x -> 0) (tan x - sin x)/x^3`
Choose the correct alternative:
`lim_(x -> 0) ("a"^x - "b"^x)/x` =
Choose the correct alternative:
If `lim_(x -> 0) (sin "p"x)/(tan 3x)` = 4, then the value of p is
