Advertisements
Advertisements
Question
Evaluate the following limits:
`lim_(x -> oo) 3/(x - 2) - (2x + 11)/(x^2 + x - 6)`
Solution
`lim_(x -> oo) 3/(x - 2) - (2x + 11)/(x^2 + x - 6) = lim_(x -> oo) (3/(x - 2) - (2x + 11)/((x + 3)(x - 2)))`
= `lim_(x -> oo) (3(x + 3) - (2x + 11))/((x + 3)(x - 2))`
= `lim_(x -> oo) (3x + 9 - 2x - 11)/((x + 3)(x - 2))`
= `lim_(x -> oo) (x - 2)/((x + 3)(x - 2))`
= `lim_(x -> oo) 1/(x + 3)`
= `1/oo`
`lim_(x -> oo) 3/(x - 2) - (2x + 11)/(x^2 + x - 6)` = 0
APPEARS IN
RELATED QUESTIONS
Evaluate the following limit:
If `lim_(x -> 1)[(x^4 - 1)/(x - 1)]` = `lim_(x -> "a")[(x^3 - "a"^3)/(x - "a")]`, find all possible values of a
Evaluate the following :
Find the limit of the function, if it exists, at x = 1
f(x) = `{(7 - 4x, "for", x < 1),(x^2 + 2, "for", x ≥ 1):}`
Evaluate the following :
Given that 7x ≤ f(x) ≤ 3x2 – 6 for all x. Determine the value of `lim_(x -> 3) "f"(x)`
Evaluate the following :
`lim_(x -> 0) [(sqrt(1 - cosx))/x]`
In exercise problems 7 – 15, use the graph to find the limits (if it exists). If the limit does not exist, explain why?
`lim_(x -> 3) 1/(x - 3)`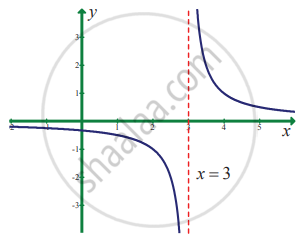
Sketch the graph of a function f that satisfies the given value:
f(– 2) = 0
f(2) = 0
`lim_(x -> 2) f(x)` = 0
`lim_(x -> 2) f(x)` does not exist.
Evaluate the following limits:
`lim_(x -> 2) (1/x - 1/2)/(x - 2)`
Evaluate the following limits:
`lim_(x -> 1) (sqrt(x) - x^2)/(1 - sqrt(x))`
Evaluate the following limits:
`lim_(x -> 5) (sqrt(x - 1) - 2)/(x - 5)`
Show that `lim_("n" -> oo) 1/1.2 + 1/2.3 + 1/3.4 + ... + 1/("n"("n" + 1))` = 1
Evaluate the following limits:
`lim_(x -> oo)(1 + 1/x)^(7x)`
Evaluate the following limits:
`lim_(x -> 0) (sin^3(x/2))/x^2`
Evaluate the following limits:
`lim_(x -> 0) (sqrt(1 + sinx) - sqrt(1 - sinx))/tanx`
Evaluate the following limits:
`lim_(x -> oo) ((x^2 - 2x + 1)/(x^2 -4x + 2))^x`
Choose the correct alternative:
`lim_(x -> 0) sqrt(1 - cos 2x)/x`
If `lim_(x -> 1) (x + x^2 + x^3|+ .... + x^n - n)/(x - 1)` = 820, (n ∈ N) then the value of n is equal to ______.
`lim_(x→-1) (x^3 - 2x - 1)/(x^5 - 2x - 1)` = ______.
