Advertisements
Advertisements
Question
Evaluate the following limits:
`lim_(x -> oo) (1 + x - 3x^3)/(1 + x^2 +3x^3)`
Solution
`lim_(x -> oo) (1 + x - 3x^3)/(1 + x^2 +3x^3) = lim_(x - oo) (x^3(1/x^3 + x/x^3 - 3))/(x^3 (1/x^3 + x^2/x^3 + 3))`
= `lim_(x -> oo) ((1/x^3 + 1/x^2 - 3)/(1/x^3 + 1/x + 3))`
= `((1/oo + 1/oo - 3)/(1/oo + 1/oo + 3))`
= `(0 + 0 - 3)/(0 + 0 + 3)`
= `(-3)/3`
`lim_(x -> oo) (1 + x - 3x^3)/(1 + x^2 +3x^3)` = – 1
APPEARS IN
RELATED QUESTIONS
Evaluate the following limit :
`lim_(x -> 7)[((root(3)(x) - root(3)(7))(root(3)(x) + root(3)(7)))/(x - 7)]`
Evaluate the following limit :
If `lim_(x -> 5) [(x^"k" - 5^"k")/(x - 5)]` = 500, find all possible values of k.
Evaluate the following :
`lim_(x -> 0)[x/(|x| + x^2)]`
Evaluate the following :
Find the limit of the function, if it exists, at x = 1
f(x) = `{(7 - 4x, "for", x < 1),(x^2 + 2, "for", x ≥ 1):}`
In problems 1 – 6, using the table estimate the value of the limit
`lim_(x -> - 3) (sqrt(1 - x) - 2)/(x + 3)`
| x | – 3.1 | – 3.01 | – 3.00 | – 2.999 | – 2.99 | – 2.9 |
| f(x) | – 0.24845 | – 0.24984 | – 0.24998 | – 0.25001 | – 0.25015 | – 0.25158 |
In exercise problems 7 – 15, use the graph to find the limits (if it exists). If the limit does not exist, explain why?
`lim_(x -> 5) |x - 5|/(x - 5)`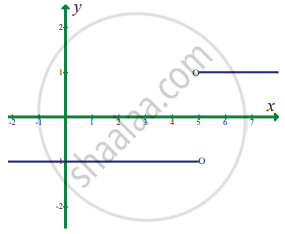
In exercise problems 7 – 15, use the graph to find the limits (if it exists). If the limit does not exist, explain why?
`lim_(x -> 0) sec x`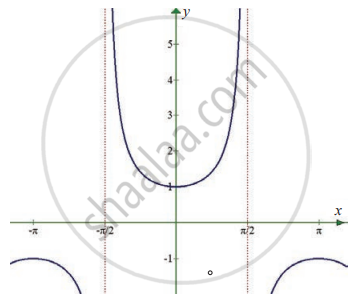
Evaluate the following limits:
`lim_(x -> 1) (root(3)(7 + x^3) - sqrt(3 + x^2))/(x - 1)`
Find the left and right limits of f(x) = `(x^2 - 4)/((x^2 + 4x+ 4)(x + 3))` at x = – 2
Evaluate the following limits:
`lim_(x -> 0) (sinalphax)/(sinbetax)`
Evaluate the following limits:
`lim_(x -> 0) (2 "arc"sinx)/(3x)`
Evaluate the following limits:
`lim_(x -> oo) x [3^(1/x) + 1 - cos(1/x) - "e"^(1/x)]`
Evaluate the following limits:
`lim_(x -> 0) (sqrt(2) - sqrt(1 + cosx))/(sin^2x)`
Evaluate the following limits:
`lim_(x -> 0) ("e"^x - "e"^(-x))/sinx`
Evaluate the following limits:
`lim_(x -> 0) (tan x - sin x)/x^3`
Choose the correct alternative:
`lim_(x -> 3) [x]` =
Choose the correct alternative:
`lim_(x -> oo) (1/"n"^2 + 2/"n"^2 + 3/"n"^2 + ... + "n"/"n"^2)` is
If `lim_(x -> 1) (x + x^2 + x^3|+ .... + x^n - n)/(x - 1)` = 820, (n ∈ N) then the value of n is equal to ______.
The value of `lim_(x→0)(sin(ℓn e^x))^2/((e^(tan^2x) - 1))` is ______.
