Advertisements
Advertisements
Question
At the given point x0 discover whether the given function is continuous or discontinuous citing the reasons for your answer:
x0 = 3, `f(x) = {{:((x^2 - 9)/(x - 3)",", "if" x ≠ 3),(5",", "if" x = 3):}`
Solution
`lim_(x -> 3^-) f(x) = lim_(x -> 3^-) (x^2 - 9)/(x - 3)`
= `lim_(x -> 3^-) ((x + 3)(x - 3))/(x - 3)`
= `lim_(x -> 3^-) (x + 3)`
= 3 + 3
= 6 .........(1)
`lim_(x -> 3^+) f(x) = lim_(x -> 3^+) (x^2 - 9)/(x - 3)`
= `lim_(x -> 3^+) ((x + 3)(x - 3))/(x - 3)`
= `lim_(x -> 3^+) (x + 3)`
= 3 + 3
= 6 .........(2)
From equations (1) and (2)
`lim_(x -> 3^-) f(x) = lim_(x -> 3^-) f(x)` = 6
∴ `lim_(x -> 3) f(x)` = 6 ........(3)
`f(3)` = 5 ........(4)
From equations (3) and (4) we have
`lim_(x -> 3) f(x) ≠ f(3)`
∴ f(x) is not continuous at x0 = 3.
APPEARS IN
RELATED QUESTIONS
Prove that f(x) = 2x2 + 3x - 5 is continuous at all points in R
Examine the continuity of the following:
x + sin x
Examine the continuity of the following:
x2 cos x
Examine the continuity of the following:
`(x^2 - 16)/(x + 4)`
Examine the continuity of the following:
|x + 2| + |x – 1|
Examine the continuity of the following:
`|x - 2|/|x + 1|`
Find the points of discontinuity of the function f, where `f(x) = {{:(x + 2",", "if", x ≥ 2),(x^2",", "if", x < 2):}`
Find the points of discontinuity of the function f, where `f(x) = {{:(x^3 - 3",", "if" x ≤ 2),(x^2 + 1",", "if" x < 2):}`
Find the points of discontinuity of the function f, where `f(x) = {{:(sinx",", 0 ≤ x ≤ pi/4),(cos x",", pi/4 < x < pi/2):}`
For what value of `alpha` is this function `f(x) = {{:((x^4 - 1)/(x - 1)",", "if" x ≠ 1),(alpha",", "if" x = 1):}` continuous at x = 1?
If f and g are continuous functions with f(3) = 5 and `lim_(x -> 3) [2f(x) - g(x)]` = 4, find g(3)
Consider the function `f(x) = x sin pi/x`. What value must we give f(0) in order to make the function continuous everywhere?
State how continuity is destroyed at x = x0 for the following graphs.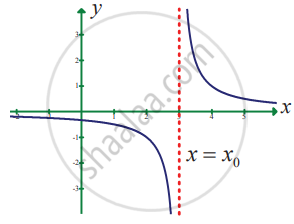
State how continuity is destroyed at x = x0 for the following graphs.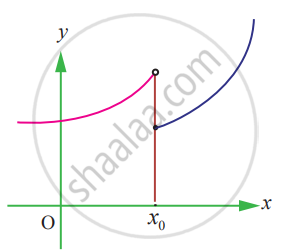
Choose the correct alternative:
Let the function f be defined by `f(x) = {{:(3x, 0 ≤ x ≤ 1),(-3 + 5, 1 < x ≤ 2):}`, then
Choose the correct alternative:
If f : R → R is defined by `f(x) = [x - 3] + |x - 4|` for x ∈ R then `lim_(x -> 3^-) f(x)` is equal to
Choose the correct alternative:
The function `f(x) = {{:((x^2 - 1)/(x^3 + 1), x ≠ - 1),("P", x = -1):}` is not defined for x = −1. The value of f(−1) so that the function extended by this value is continuous is
Choose the correct alternative:
Let f be a continuous function on [2, 5]. If f takes only rational values for all x and f(3) = 12, then f(4.5) is equal to
