Advertisements
Advertisements
प्रश्न
Evaluate the following limits:
`lim_(x -> pi) (1 + sinx)^(2"cosec"x)`
उत्तर
`lim_(x -> pi) (1 + sinx)^(2"cosec"x) = lim_(x -> pi)(1 + sinx)^(2/sinx)`
Put y = sin x
When x = `pi/2` the y = `sin pi/2` = 1
`lim_(x -> pi) (1 + sinx)^(2"cosec"x) = lim_(y ->1)(1 +y)^(2/y)`
= `(1 + 1)^(2/1)`
= 22
= 4
APPEARS IN
संबंधित प्रश्न
Evaluate the following limit:
`lim_(x -> 5)[(x^3 - 125)/(x^5 - 3125)]`
Evaluate the following limit:
If `lim_(x -> 1)[(x^4 - 1)/(x - 1)]` = `lim_(x -> "a")[(x^3 - "a"^3)/(x - "a")]`, find all possible values of a
In the following example, given ∈ > 0, find a δ > 0 such that whenever, |x – a| < δ, we must have |f(x) – l| < ∈.
`lim_(x -> 1) (x^2 + x + 1)` = 3
Evaluate the following :
`lim_(x -> 0) [(sqrt(1 - cosx))/x]`
In problems 1 – 6, using the table estimate the value of the limit
`lim_(x -> - 3) (sqrt(1 - x) - 2)/(x + 3)`
| x | – 3.1 | – 3.01 | – 3.00 | – 2.999 | – 2.99 | – 2.9 |
| f(x) | – 0.24845 | – 0.24984 | – 0.24998 | – 0.25001 | – 0.25015 | – 0.25158 |
In exercise problems 7 – 15, use the graph to find the limits (if it exists). If the limit does not exist, explain why?
`lim_(x -> 3) (4 - x)`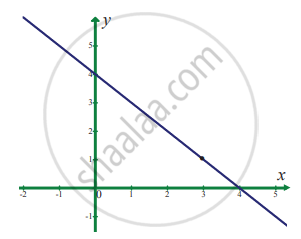
In exercise problems 7 – 15, use the graph to find the limits (if it exists). If the limit does not exist, explain why?
`lim_(x -> 1) (x^2 + 2)`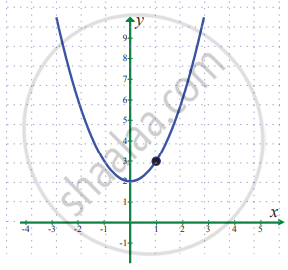
Sketch the graph of f, then identify the values of x0 for which `lim_(x -> x_0)` f(x) exists.
f(x) = `{{:(x^2",", x ≤ 2),(8 - 2x",", 2 < x < 4),(4",", x ≥ 4):}`
Write a brief description of the meaning of the notation `lim_(x -> 8) f(x)` = 25
If the limit of f(x) as x approaches 2 is 4, can you conclude anything about f(2)? Explain reasoning
Evaluate the following limits:
`lim_(sqrt(x) -> 3) (x^2 - 81)/(sqrt(x) - 3)`
Evaluate the following limits:
`lim_(x -> "a") (sqrt(x - "b") - sqrt("a" - "b"))/(x^2 - "a"^2) ("a" > "b")`
Evaluate the following limits:
`lim_(x -> 3) (x^2 - 9)/(x^2(x^2 - 6x + 9))`
Choose the correct alternative:
`lim_(x -> 0) (x"e"^x - sin x)/x` is
Choose the correct alternative:
If `lim_(x -> 0) (sin "p"x)/(tan 3x)` = 4, then the value of p is
Choose the correct alternative:
`lim_(x -> oo) (1/"n"^2 + 2/"n"^2 + 3/"n"^2 + ... + "n"/"n"^2)` is
Choose the correct alternative:
The value of `lim_(x -> 0) sinx/sqrt(x^2)` is
`lim_(x→0^+)(int_0^(x^2)(sinsqrt("t"))"dt")/x^3` is equal to ______.
`lim_(x→∞)((x + 7)/(x + 2))^(x + 4)` is ______.
The value of `lim_(x→0)(sin(ℓn e^x))^2/((e^(tan^2x) - 1))` is ______.
