Question

sin [cot^–1 (cos (tan^–1 x))] = ______.

पर्याय

• `sqrt((x^2 - 1)/(x^2 + 2))`

• `sqrt((x - 2)/(x^2 + 1))`

• `sqrt((x^2 + 1)/(x^2 + 2))`

• `1/sqrt(x^2 - 1)`

Answer 1

sin [cot^–1 (cos (tan^–1 x))] = `underlinebb(sqrt((x^2 + 1)/(x^2 + 2)))`.

Explanation:

Let tan^–1 x = y   ...(i)

tan y `\implies` tan y = y = x / 1

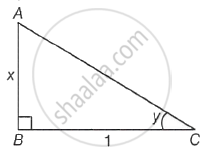
In ΔABC,

tan y = AB / BC = x

By Pythagoras theorem,

AC² = AB² + BC²

`\implies` AC² = x² + 1² = x² + 1

`\implies` AC = `sqrt(x^2 + 1)`

∴ cos y = `(BC)/(AC) = 1/sqrt(x^2 + 1)`  ...(ii)

`\implies` y = `cos^-1(1/sqrt(x^2 + 1))`

Now, 

let cot^–1 (cos (y)) = z  ...(iii)

cot z = cos y

`\implies` cot z = `1/sqrt(x^2 + 1)`  ...[Using equation (ii)]

`\implies` z = `cot^-1 (1/sqrt(x^2 + 1))`

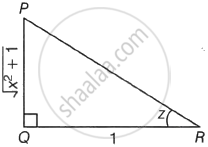
In ΔPQR,

cot z = `(QR)/(PQ) = 1/sqrt(x^2 + 1)`

By Pythagoras theorem,

PR² = PQ² + QR²

∴ PR = `sqrt(x^2 + 2)`

So, sin z = `sqrt(x^2 + 1)/sqrt(x^2 + 2)`  ...[Using equations (i) and (iii)]

∴ sin [cot^–1 (cos (tan^–1 x))] = `sqrt((x^2 + 1)/(x^2 + 2))`