Advertisements
Advertisements
प्रश्न
समीपी तारों की दूरियाँ ज्ञात करने के लिए लंबन के सिद्धांत का प्रयोग किया जाता है। सूर्य के परितः अपनी कक्षा में छः महीनों के अन्तराल पर पृथ्वी की अपनी, दो स्थानों को मिलाने वाली, आधार रेखा AB है। अर्थात आधार रेखा पृथ्वी की कक्षा के व्यास ≈ 3x 1011 m के लगभग बराबर है। लेकिन चूंकि निकटतम तारे भी इतने अधिक दूर हैं कि इतनी लंबी आधार रेखा होने पर भी वे चाप के केवल 1″ (सेकंड, चाप का) की कोटि का लंबन प्रदर्शित करते हैं। खगोलीय पैमाने पर लंबाई का सुविधाजनक मात्रक पारसेक है। यह किसी पिण्ड की वह दूरी है जो पृथ्वी से सूर्य तक की दूरी के बराबर आधार रेखा के दो विपरीत किनारों से चाप के 1′ का लंबन प्रदर्शित करती है। मीटरों में एक पारसेक कितना होता है?
उत्तर
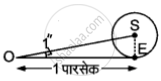
चित्र में S सूर्य तथा E पृथ्वी है। बिंदु O की पृथ्वी से दूरी 1 पारसेक है। पृथ्वी की कक्षा की त्रिज्या `"SE" = "व्यास"/2`
या `"SE" = (3 xx 10^11 "m")/2 = 1.5 xx 10^11 "m"`
प्रश्नानुसार रेखाखंड SE, बिंदु O पर 1" (चाप का) कोण अंतरित करता है।
अतः `angle"SOE"` = 1" = `(1/(60 xx 60)) "डिग्री"`
= `1/(60 xx 60) xx pi/180 "rad" [∵ 180^circ = pi " rad"]`
∵ ∠SOE बहुत छोटा है, अतः दिशाएँ OS तथा OE लगभग सम्पाती होगी।
∴ दूरी SE को वृत्तीय चाप तथा दूरी OE को त्रिज्या व O को केंद्र माना जा सकता है।
∠SOE (rad. में) = `("चाप" "SE") / ("त्रिज्या" "SE")`
या `1/(60 xx 60) xx pi/180 = (1.5 xx 10^11 "m")/(1 "पारसेक")`
= `1 "पारसेक" = (1.5 xx 10^11 xx 60 xx 60 xx 180)/pi "m"`
= `(1.5 xx 60 xx 60 xx 180 xx 10^11)/3.14 "m"`
= `309.55 xx 10^14 ` m
अतः 1 पारसेक = `3.0 xx 10^16` m के बराबर होता है।
APPEARS IN
संबंधित प्रश्न
हमारे सौर परिवार से निकटतम तारा 4.29 प्रकाश वर्ष दूर है। पारसेक में यह दूरी कितनी है? यह तारा (ऐल्फा सेटौरी नामक) तब कितना लम्बन प्रदर्शित करेगा जब इसे सूर्य के परितः अपनी कक्षा में पृथ्वी के दो स्थानों से जो छः महीने के अन्तराल पर हैं, देखा, जाएगा?
यह एक विख्यात तथ्य है कि पूर्ण सूर्यग्रहण की अवधि में चंद्रमा की चक्रिका सूर्य की चक्रिका को पूरी तरह ढक लेती है। चंद्रमा का लगभग व्यास ज्ञात कीजिए।
(पृथ्वी से चंद्रमा की दूरी = 3.84 × 108 m सूर्य का कोणीय व्यास = 1920′ )
