Advertisements
Advertisements
प्रश्न
संलग्न आकृति में रेख MN ‘O’ केंद्रवाले वृत्त की जीवा है। MN = 25, जीवा MN पर बिंदु L इस प्रकार है कि, ML = 9 और d(O, L) = 5 तो इस वृत्त की त्रिज्या ज्ञात कीजिए।
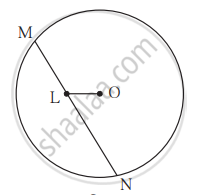
उत्तर १
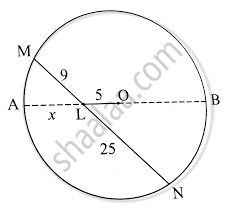
रेख OL को इस तरह बढ़ाओ कि, वह वृत्त को बिंदु A तथा B पर इस प्रकार प्रतिच्छेदित करता है कि, A-L-O तथा L-O-B.
ML = 9, OL = 5, MN = 25 ...............(दत्त)
ML + LN = MN ...........(M-L-N)
∴ 9 + LN = 25
∴ LN = 25 - 9
∴ LN = 16
मानो, AL = x
OA = OL + LA ...............(O-L-A)
∴ OA = (5 + x)
OB = OA ...........(एक ही वृत्त की त्रिज्याएँ)
∴ OB = (5 + x)
LB = LO + OB ..........(L-O-B)
∴ LB = 5 + (5 + x)
∴ LB = (10 + x)
जीवा AB तथा जीवा MN वृत्त के अंतः भाग में बिंदु L पर प्रतिच्छेदित करते है |
∴ जीवाओं के अंतःछेदन प्रमेय से,
AL × LB = ML × LN
∴ x × (10 + x) = 9 × 16
∴ 10x + x2 = 144
∴ x2 + 10x - 144 = 0
∴ x2 + 18x - 8x - 144 = 0
∴ x(x + 18) - 8(x + 18) = 0
∴ (x + 18)(x - 18) = 0
∴ x + 18 = 0 या x - 8 = 0
∴ x = -18 या x = 8
∵ किसी रेषाखंड की लंबाई ऋणात्मक नहीं हो सकती है |
∴ x = -18 यह अमान्य है |
∴ x = 8
त्रिज्या = OA = 5 + x = 5 + 8 = 13
वृत्त की त्रिज्या 13 है |
उत्तर २
वैकल्पिक विधि :

रेख OX ⊥ जीवा MN
इस प्रकार खींचो कि, M-X-N.
रेख ON खींचो |
रेख OX ⊥ जीवा MN.
वृत्त के केंद्र से जीवा पर डाला गया लंब जीवा को समद्विभाजित करता है |
∴ MX = XN = `1/2`MN
∴ MX = XN = `1/2 xx 25`
∴ MX = XN = 12.5 ...............(1)
ML + LX = MX ............(M-L-X)
∴ 9 + LX = 12.5 .............[(1) से]
∴ LX = 12.5 - 9
∴ LX = 3.5
ΔOXL में,
∠OXL = 90° ..........(रचना)
∴ पायथागोरस के प्रमेय से,
`"OL"^2 = "OX"^2 + "LX"^2`
∴ `5^2 = "OX"^2 + 3.5^2`
∴ `"OX"^2 = 5^2 - 3.5^2`
∴ `"OX"^2 = 25 - 12.25`
∴ `"OX"^2 = 12.75` ...........(2)
ΔOXN में,
∠OXN = 90° ..........(रचना)
∴ पायथागोरस के प्रमेय से,
`"ON"^2 = "OX"^2 + "XN"^2`
∴ `"ON"^2 = 12.75 + 12.5^2`
∴ `"ON"^2 = 12.75 + 156.25`
∴ `"ON"^2 = 169`
∴ ON = 13 ............(दोनों पक्षों का वर्गमूल लेने पर)
∴ वृत्त की त्रिज्या = ON = 13
वृत्त की त्रिज्या 13 है |
APPEARS IN
संबंधित प्रश्न
4.5 सेमी त्रिज्या वाले वृत्त की दो स्पर्श रेखाएँ परस्पर समांतर हैं। उन स्पर्श रेखाओं के बीच की दूरी कितनी होगी कारण सहित लिखिए।
दिए गए प्रत्येक उप प्रश्न के लिए चार वैकल्पिक उत्तर दिए हैं। उनमें से उचित विकल्प चुनकर लिखिए।
परस्पर प्रतिच्छेदित करने वाले दो वृत्त एक दूसरे के केंद्र से होकर जाते हैं। यदि उनके केंद्रों के बीच की दूरी 12 सेमी हो, तो प्रत्येक वृत्त की त्रिज्या कितने सेमी होगी?
दिए गए प्रत्येक उप प्रश्न के लिए चार वैकल्पिक उत्तर दिए हैं। उनमें से उचित विकल्प चुनकर लिखिए।
यदि किसी वृत्त के केंद्र से 12.5 सेमी की दूरी पर स्थित किसी बिंदु से उस वृत्त पर खींची गई स्पर्श रेखाखंड की लंबाई 12 सेमी हो, तो उस वृत्त का व्यास कितने सेमी होगा?
निम्नलिखित प्रश्न में वृत्त का समीकरण ज्ञात कीजिए:
केंद्र (0, 2) और त्रिज्या 2 इकाई
निम्नलिखित प्रश्न में से वृत्त का केंद्र और त्रिज्या ज्ञात कीजिए:
x2 + y2 – 8x + 10y – 12 = 0
निम्नलिखित प्रश्न में से वृत्त का केंद्र और त्रिज्या ज्ञात कीजिए:
2x2 + 2y2 – x = 0
बिंदुओं (4, 1) और (6, 5) से जाने वाले वृत्त का समीकरण कीजिए जिसका केंद्र रेखा 4x + y = 16 पर स्थित है।
त्रिज्या 5 के उस वृत्त का समीकरण ज्ञात कीजिए जिसका केंद्र x-अक्ष पर हो और जो बिंदु (2, 3) से जाता है।
क्या बिंदु (−2.5, 3.5) वृत्त x2 + y2 = 25 के अंदर, बाहर या वृत्त पर स्थित है?
यदि वृत्त की त्रिज्या 5 सेमी हो, तो उस वृत्त की सबसे बड़ी जीवा की लंबाई ज्ञात कीजिए।
