Advertisements
Advertisements
प्रश्न
Solve the following systems of inequations graphically:
x + 2y ≤ 40, 3x + y ≥ 30, 4x + 3y ≥ 60, x ≥ 0, y ≥ 0
उत्तर
Converting the inequations to equations, we obtain:
x + 2y = 40, 3x + y = 30, 4x + 3y = 60
x + 2y = 40: This line meets the x-axis at (40, 0) and y-axis at (0, 20). Draw a thick line through these points.
We see that the origin (0,0) satisfies the inequation x + 2y\[\leq\]40
Therefore, the region containing the origin is the solution of the inequality x + 2y \[\leq\] 40
3x + y = 30: This line meets the x-axis at (10, 0) and y-axis at (0, 30). Draw a thick line through these points.
We see that the origin (0, 0) does not satisfy the inequation 3x + y\[\geq\] 30
Therefore, the region that does not contain the origin is the solution of the inequality 3x+ y\[\geq\] 30
4x + 3y = 60: This line meets the x-axis at (15, 0) and y-axis at (0, 20). Draw a thick line through these points.
We see that the origin (0, 0) does not satisfy the inequation x + 3y \[\geq\] 60 Therefore, the region that does not contain the origin is the solution of the inequality
4x + 3y\[\geq\]60
Also, x ≥ 0, y ≥ 0 represents the first quadrant. So, the solution set must be in the first quadrant.
Hence, the solution to the inequalities is the intersection of the above three solutions. Thus, the shaded region represents the solution set of the given set of inequalities.

APPEARS IN
संबंधित प्रश्न
Solve the given inequality graphically in two-dimensional plane: x + y < 5
Solve the given inequality graphically in two-dimensional plane: 2x + y ≥ 6
Solve the given inequality graphically in two-dimensional plane: 3x + 4y ≤ 12
Solve the given inequality graphically in two-dimensional plane: y + 8 ≥ 2x
Solve the given inequality graphically in two-dimensional plane: x – y ≤ 2
Solve the given inequality graphically in two-dimensional plane: 2x – 3y > 6
Solve the given inequality graphically in two-dimensional plane: –3x + 2y ≥ –6
Solve the given inequality graphically in two-dimensional plane: 3y – 5x < 30
Solve the given inequality graphically in two-dimensional plane: y < –2
Solve the given inequality graphically in two-dimensional plane: x > –3
Solve the inequalities and represent the solution graphically on number line:
5x + 1 > –24, 5x – 1 < 24
Solve the inequality and represent the solution graphically on number line:
2(x – 1) < x + 5, 3(x + 2) > 2 – x
Solve the following inequalities and represent the solution graphically on number line:
3x – 7 > 2(x – 6), 6 – x > 11 – 2x
How many litres of water will have to be added to 1125 litres of the 45% solution of acid so that the resulting mixture will contain more than 25% but less than 30% acid content?
IQ of a person is given by the formula
IQ = `(MA)/(CA) xx100`
Where MA is mental age and CA is chronological age. If 80 ≤ IQ ≤ 140 for a group of 12 years old children, find the range of their mental age.
Solve the following systems of linear inequation graphically:
2x + 3y ≤ 6, x + 4y ≤ 4, x ≥ 0, y ≥ 0
Solve the following systems of linear inequations graphically:
x − y ≤ 1, x + 2y ≤ 8, 2x + y ≥ 2, x ≥ 0, y ≥ 0
Solve the following systems of linear inequations graphically:
x + y ≥ 1, 7x + 9y ≤ 63, x ≤ 6, y ≤ 5, x ≥ 0, y ≥ 0
Solve the following systems of linear inequations graphically:
2x + 3y ≤ 35, y ≥ 3, x ≥ 2, x ≥ 0, y ≥ 0
Show that the solution set of the following linear inequations is empty set:
x + 2y ≤ 3, 3x + 4y ≥ 12, y ≥ 1, x ≥ 0, y ≥ 0
Find the linear inequations for which the shaded area in Fig. 15.41 is the solution set. Draw the diagram of the solution set of the linear inequations:
Show that the solution set of the following linear in equations is an unbounded set:
x + y ≥ 9
3x + y ≥ 12
x ≥ 0, y ≥ 0
Solve the following systems of inequations graphically:
12x + 12y ≤ 840, 3x + 6y ≤ 300, 8x + 4y ≤ 480, x ≥ 0, y ≥ 0
Solve the following systems of inequations graphically:
5x + y ≥ 10, 2x + 2y ≥ 12, x + 4y ≥ 12, x ≥ 0, y ≥ 0
Show that the solution set of the following system of linear inequalities is an unbounded region:
\[2x + y \geq 8, x + 2y \geq 10, x \geq 0, y \geq 0\]
Mark the correct alternative in each of the following:
If x\[<\]7, then
Find the linear inequalities for which the shaded region in the given figure is the solution set.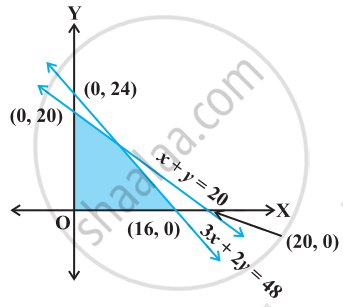
State which of the following statement is True or False.
If x < y and b < 0, then `x/"b" < y/"b"`
State which of the following statement is True or False.
If xy > 0, then x < 0 and y < 0
Graph of x ≥ 0 is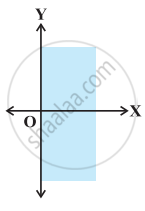
Graph of y ≤ 0 is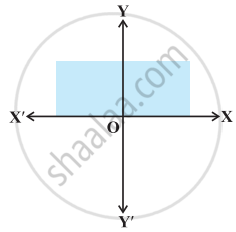
Solution set of x + y ≥ 0 is