Advertisements
Advertisements
प्रश्न
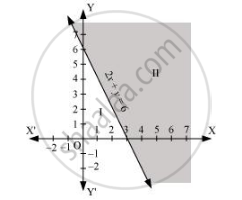
Solve the given inequality graphically in two-dimensional plane: 2x + y ≥ 6
उत्तर
The graphical representation of 2x + y = 6 is given in the figure below.
This line divides the xy-plane in two half planes, I and II.
Select a point (not on the line), which lies in one of the half planes, to determine whether the point satisfies the given inequality or not.
We select the point as (0, 0).
It is observed that,
2(0) + 0 ≥ 6 or 0 ≥ 6, which is false
Therefore, half plane I is not the solution region of the given inequality. Also, it is evident that any point on the line satisfies the given inequality.
Thus, the solution region of the given inequality is the shaded half plane II including the points on the line.
This can be represented as follows.
APPEARS IN
संबंधित प्रश्न
Solve the given inequality graphically in two-dimensional plane: x + y < 5
Solve the given inequality graphically in two-dimensional plane: 3x + 4y ≤ 12
Solve the given inequality graphically in two-dimensional plane: y + 8 ≥ 2x
Solve the given inequality graphically in two-dimensional plane: 2x – 3y > 6
Solve the given inequality graphically in two-dimensional plane: 3y – 5x < 30
Solve the given inequality graphically in two-dimensional plane: y < –2
Solve the inequalities and represent the solution graphically on number line:
5x + 1 > –24, 5x – 1 < 24
Solve the inequality and represent the solution graphically on number line:
2(x – 1) < x + 5, 3(x + 2) > 2 – x
Solve the following inequalities and represent the solution graphically on number line:
3x – 7 > 2(x – 6), 6 – x > 11 – 2x
A solution is to be kept between 68° F and 77° F. What is the range in temperature in degree Celsius (C) if the Celsius/Fahrenheit (F) conversion formula is given by `F= 9/8` C + 32?
How many litres of water will have to be added to 1125 litres of the 45% solution of acid so that the resulting mixture will contain more than 25% but less than 30% acid content?
Solve the following systems of linear inequation graphically:
2x + 3y ≤ 6, 3x + 2y ≤ 6, x ≥ 0, y ≥ 0
Solve the following systems of linear inequation graphically:
2x + 3y ≤ 6, x + 4y ≤ 4, x ≥ 0, y ≥ 0
Solve the following systems of linear inequations graphically:
x − y ≤ 1, x + 2y ≤ 8, 2x + y ≥ 2, x ≥ 0, y ≥ 0
Solve the following systems of linear inequations graphically:
2x + 3y ≤ 35, y ≥ 3, x ≥ 2, x ≥ 0, y ≥ 0
Show that the solution set of the following linear inequations is empty set:
x − 2y ≥ 0, 2x − y ≤ −2, x ≥ 0, y ≥ 0
Show that the solution set of the following linear inequations is empty set:
x + 2y ≤ 3, 3x + 4y ≥ 12, y ≥ 1, x ≥ 0, y ≥ 0
Find the linear inequations for which the solution set is the shaded region given in Fig. 15.42
Show that the solution set of the following linear in equations is an unbounded set:
x + y ≥ 9
3x + y ≥ 12
x ≥ 0, y ≥ 0
Solve the following systems of inequations graphically:
12x + 12y ≤ 840, 3x + 6y ≤ 300, 8x + 4y ≤ 480, x ≥ 0, y ≥ 0
Solve the following systems of inequations graphically:
x + 2y ≤ 40, 3x + y ≥ 30, 4x + 3y ≥ 60, x ≥ 0, y ≥ 0
Solve the following systems of inequations graphically:
5x + y ≥ 10, 2x + 2y ≥ 12, x + 4y ≥ 12, x ≥ 0, y ≥ 0
Show that the solution set of the following system of linear inequalities is an unbounded region:
\[2x + y \geq 8, x + 2y \geq 10, x \geq 0, y \geq 0\]
Mark the correct alternative in each of the following:
If x\[<\]7, then
Write the solution of the inequation\[\frac{x^2}{x - 2} > 0\]
Find the linear inequalities for which the shaded region in the given figure is the solution set.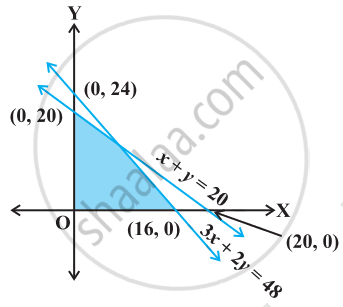
State which of the following statement is True or False.
If x < y and b < 0, then `x/"b" < y/"b"`
State which of the following statement is True or False.
If xy > 0, then x > 0 and y < 0
State which of the following statement is True or False.
If xy > 0, then x < 0 and y < 0
Graph of x < 3 is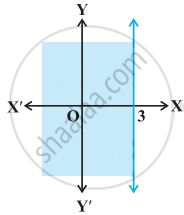
Graph of y ≤ 0 is