Advertisements
Advertisements
प्रश्न
Solve the following problem.
In olden days, while laying the rails for trains, small gaps used to be left between the rail sections to allow for thermal expansion. Suppose the rails are laid at room temperature 27 °C. If maximum temperature in the region is 45 °C and the length of each rail section is 10 m, what should be the gap left given that α = 1.2 × 10–5K–1 for the material of the rail section?
उत्तर
Given: T1 = 27 °C, T2 = 45 °C, L1 = 10 m. α = 1.2 × 10–5 / K
To find: Gap that should be left (L2 – L1)
Formula: L2 – L1 = L1 α (T2 - T1)
Calculation: From formula,
L2 - L1 = 10 × 1.2 × 10–5 × (45 - 27)
= 2.16 × 10–3 m
= 2.16 mm
The gap that should be left between rail sections is 2.16 mm.
APPEARS IN
संबंधित प्रश्न
Is it possible for two bodies to be in thermal equilibrium if they are not in contact?
A system X is neither in thermal equilibrium with Y nor with Z. The systems Y and Z
For a constant-volume gas thermometer, one should fill the gas at
The density of water at 0°C is 0.998 g cm–3 and at 4°C is 1.000 g cm–1. Calculate the average coefficient of volume expansion of water in the temperature range of 0 to 4°C.
A glass flask has a volume 1 × 10−4 m3. It is filled with a liquid at 30°C. If the temperature of the system is raised to 100°C, how much of the liquid will overflow? (Coefficient of volume expansion of glass is 1.2 × 10−5 (°C)−1 while that of the liquid is 75 × 10−5 (°C)−1).
A clock pendulum having coefficient of linear expansion. α = 9 × 10-7/°C-1 has a period of 0.5 s at 20°C. If the clock is used in a climate, where the temperature is 30°C, how much time does the clock lose in each oscillation? (g = constant)
A metal rod of Young's moduls 'Y' and coefficient of linear expansion 'a' has its temeprature raised by 'Δ θ'. The linear stress to prevent the expansion of rod is ______.
(L and l is original length of rod and expansion respectively)
A metal rod of cross-sectional area 3 × 10-6 m2 is suspended vertically from one end has a length 0.4 m at 100°C. Now the rod is cooled upto 0°C, but prevented from contracting by attaching a mass 'm' at the lower end. The value of 'm' is ______.
(Y = 1011 N/m2, coefficient of linear expansion = 10-5/K, g = 10m/s2)
A metal rod of length Land cross-sectional area A is heated through T °C. What is the force required to prevent the expansion of the rod lengthwise?
(Y = Young's modulus of material of the rod, α = coefficient of linear expansion of the rod.)
The volume of a metal block changes by 0.86% when heated through 200 °C then its coefficient of cubical expansion is ______.
A bimetallic strip is made of aluminium and steel (αAl > αsteel) . On heating, the strip will ______.
As the temperature is increased, the time period of a pendulum ______.
The radius of a metal sphere at room temperature T is R, and the coefficient of linear expansion of the metal is α. The sphere is heated a little by a temperature ∆T so that its new temperature is T + ∆T. The increase in the volume of the sphere is approximately ______.
A student records the initial length l, change in temperature ∆T and change in length ∆l of a rod as follows:
| S.No. | l(m) | ∆T (C) | ∆l (m) |
| 1. | 2 | 10 | `4 xx 10^-4` |
| 2. | 1 | 10 | `4 xx 10^-4` |
| 3. | 2 | 20 | `2 xx 10^-4` |
| 4. | 3 | 10 | `6 xx 10^-4` |
If the first observation is correct, what can you say about observations 2, 3 and 4.
Calculate the stress developed inside a tooth cavity filled with copper when hot tea at temperature of 57°C is drunk. You can take body (tooth) temperature to be 37°C and α = 1.7 × 10–5/°C, bulk modulus for copper = 140 × 109 N/m2.
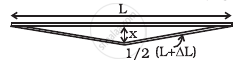
A rail track made of steel having length 10 m is clamped on a raillway line at its two ends (figure). On a summer day due to rise in temperature by 20° C, it is deformed as shown in figure. Find x (displacement of the centre) if αsteel = 1.2 × 10–5/°C.
At what temperature a gold ring of diameter 6.230 cm be heated so that it can be fitted on a wooden bangle of diameter 6.241 cm? Both diameters have been measured at room temperature (27°C). (Given: coefficient of linear thermal expansion of gold αL = 1.4 × 10-5 K-1).
Each side of a box made of metal sheet in cubic shape is 'a' at room temperature 'T', the coefficient of linear expansion of the metal sheet is 'α'. The metal sheet is heated uniformly, by a small temperature ΔT, so that its new temeprature is T + ΔT. Calculate the increase in the volume of the metal box.
If the length of a cylinder on heating increases by 2%, the area of its base will increase by ______.
Length of steel rod so that it is 5 cm longer than the copper rod at all temperatures should be ______ cm.
(α for copper = 1.7 × 10-5/°C and α for steel = 1.1 × 10-5/°C)
Given below are two statements: one is labelled as Assertion A and the other is labelled as Reason R.
- Assertion A: When a rod lying freely is heated, no thermal stress is developed in it.
- Reason R: On heating, the length of the rod increases. In light of the above statements.
choose the correct answer from the options given below:
A glass flask is filled up to a mark with 50 cc of mercury at 18°C. If the flask and contents are heated to 38°C, how much mercury will be above the mark? (α for glass is 9 × 10-6/°C and coefficient of real expansion of mercury is 180 × 10-6/°C)
A metal rod Y = 2 × 1012 dyne cm-2 of coefficient of linear expansion 1.6 × 10-5 per °C has its temperature raised by 20°C. The linear compressive stress to prevent the expansion of the rod is ______.
