Advertisements
Advertisements
प्रश्न
State Biot Savart law.
उत्तर
The magnetic induction, according to Biot Savart law, at a point P at a distance r due to current element Idl is given by
`"d"vec"B" = μ_0/(4π) . ("I"dl sin "θ")/r^2` inward as shown
In the vector form, it can be written as
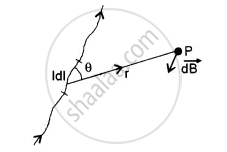
`vec"dB" = (μ_0 "I")/(4π) . ( bar(dl) xx hatr )/r^2` , θ is the angle `bar(dl)` vector and `hatr` is the position vector of the point P.
Clearly, dB ∝ I
∝ dl
∝ `l/r^2`
∝ sin θ
μ0 is the absolute permeability of free space.
APPEARS IN
संबंधित प्रश्न
An electric current I flows through an infinitely long conductor as shown in Figure 2 (a) below. Write an expression and direction for the magnetic field at point P.
A long wire with a small current element of length 1 cm is placed at the origin and carries a current of 10 A along the X-axis. Find out the magnitude and direction of the magnetic field due to the element on the Y-axis at a distance 0.5 m from it.
Derive the expression for the magnetic field due to a current carrying coil of radius r at a distance x from the centre along the X-axis.
Biot-Savart law indicates that the moving electrons (velocity v) produce a magnetic field B such that ______.
- both are long range and inversely proportional to the square of distance from the source to the point of interest.
-
both are linear in source.
-
both are produced by scalar sources.
-
both follow principle of superposition.
Biot-Savart law indicates that the moving electrons velocity (V) produce a magnetic field B such that ______.
A circular loop of radius 0.3 cm lies parallel to much bigger circular of radius 20 cm. The centre of the small loop is on the axis of the bigger loop. The distance between their centres is 15 cm. If a current of 2.0 A flows through the smaller loop, then the flux linked with the bigger loop is ______.
A current carrying loop consists of 3 identical quarter circles of radius R, lying in the positive quadrants of the x-y, y-z and z-x planes with their centres at the origin, joined together. Find the direction and magnitude of B at the origin.
Two identical circular loops P and Q, each of radius R carrying current I are kept in perpendicular planes such that they have a common centre O as shown in the figure.
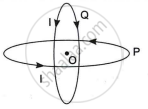
Find the magnitude and direction of the net magnetic field at point O.
