Advertisements
Advertisements
प्रश्न
Biot-Savart law indicates that the moving electrons velocity (V) produce a magnetic field B such that ______.
पर्याय
- B ∥ v.
- B ⊥ v.
- it obeys inverse cube law.
- it is along the line joining electron and point of observation.
उत्तर
Biot-Savart law indicates that the moving electrons velocity (V) produce a magnetic field B such that B ⊥ v.
Explanation:
According to the Niot-Savart law, the magnitude of `vecB` is: `B oo |q|; B oo v; B oo sin phi; B oo 1/r^2`
`B oo (|q| v sin phi)/r^2`
`B = (mu_0 |q| v sin phi)/r^2`
Where `mu_0/(4pi)` is a proportionality constant, 'r' is the magnitude of position vector from charge to that point at which we have to find the magnetic field and `pgi` is the angle between `vecv` and `vecr`.
or `vecB = (mu_0)/(4pi) (|q| (vecv xx vecr))/(|r^3|) hatn`
Where `hatn` is the direction of `vecB` which is in the direction of cross product of `vecv` and `vecr`. Or we can say that `vecB` ⊥ to both `vecv` and `vecr`.
Where is a proportionality constant, V’ is the magnitude of position vector from charge to that point at which we have to find the magnetic field and < f) is the angle between v and F.
Where h is the direction of B which is in the direction of cross product of v and F . Or we can say that B ⊥ to both v and F.
APPEARS IN
संबंधित प्रश्न
State Biot – Savart law.
A wire of length l is bent in the form of an equilateral triangle and carries an electric current i. Find the magnetic field B at the centre.
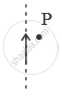
An electric current I flows through an infinitely long conductor as shown in Figure 2 (a) below. Write an expression and direction for the magnetic field at point P.
State and explain the law used to determine magnetic field at a point due to a current element. Derive the expression for the magnetic field due to a circular current carrying loop of radius r at its centre.
State Biot Savart law.
Biot-Sawart law indicates that the moving electrons (velocity `overset(->)("v")`) produce a magnetic field B such that
A current carrying loop consists of 3 identical quarter circles of radius R, lying in the positive quadrants of the x-y, y-z and z-x planes with their centres at the origin, joined together. Find the direction and magnitude of B at the origin.
Two identical circular loops P and Q, each of radius R carrying current I are kept in perpendicular planes such that they have a common centre O as shown in the figure.
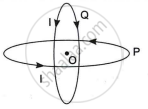
Find the magnitude and direction of the net magnetic field at point O.
Using Biot-Savart law, show that magnetic flux density 'B' at the centre of a current carrying circular coil of radius R is given by: `B = ("μ"_0I)/(2R)` where the terms have their usual meaning.
