Advertisements
Advertisements
प्रश्न
Using Biot-Savart law, show that magnetic flux density 'B' at the centre of a current carrying circular coil of radius R is given by: `B = ("μ"_0I)/(2R)` where the terms have their usual meaning.
उत्तर
Let a circular coil of radius R carry a current I and O be its centre.
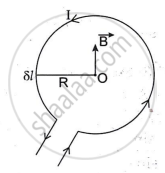
By Biot-Savart's law, the magnitude of the magnetic field at O due a small element δ l of the loop is,
`δB = "μ"_0/(4π) (Iδl sinθ)/R^2`
Where θ is the angle between the length of the element (δ l) and the line joining the element to the point O. Here, θ = 90° because every element of. a circle is perpendicular to the radius.
∴ `δB = "μ"_0/(4π) (Iδl)/R^2`
Every component of the coil will have the same field direction. Because of the complete coil, the field `vec B` magnitude at O is:
`B = "μ"_0/(4pi)I/R^2 "∑"δl`
But `"∑ "δl = 2piR`
∴ `B = "μ"_0/(4pi) · I/R^2 xx 2piR`
or `B = ("μ"_0I)/(2R)`
APPEARS IN
संबंधित प्रश्न
What does a toroid consist of? Find out the expression for the magnetic field inside a toroid for N turns of the coil having the average radius r and carrying a current I. Show that the magnetic field in the open space inside and exterior to the toroid is zero.
A long, vertical wire carrying a current of 10 A in the upward direction is placed in a region where a horizontal magnetic field of magnitude 2.0 × 10−3 T exists from south to north. Find the point where the resultant magnetic field is zero.
An electric current I flows through an infinitely long conductor as shown in Figure 2 (a) below. Write an expression and direction for the magnetic field at point P.
A long wire with a small current element of length 1 cm is placed at the origin and carries a current of 10 A along the X-axis. Find out the magnitude and direction of the magnetic field due to the element on the Y-axis at a distance 0.5 m from it.
Derive the expression for the magnetic field due to a current carrying coil of radius r at a distance x from the centre along the X-axis.
State and explain the law used to determine the magnetic field at a point due to a current element. Derive the expression for the magnetic field due to a circular current-carrying loop of radius r at its center.
A straight wire carrying a current of 5 A is bent into a semicircular arc radius 2 cm as shown in the figure. Find the magnitude and direction of the magnetic field at the center of the arc

A square shaped current carrying loop MNOP is placed near a straight long current carrying wire AB as shown in the fig. The wire and the loop lie in the same plane. If the loop experiences a net force F towards the wire, find the magnitude of the force on the side 'NO' of the loop.

- both are long range and inversely proportional to the square of distance from the source to the point of interest.
-
both are linear in source.
-
both are produced by scalar sources.
-
both follow principle of superposition.
Biot-Sawart law indicates that the moving electrons (velocity `overset(->)("v")`) produce a magnetic field B such that
