Advertisements
Advertisements
प्रश्न
Using Biot-Savart law, show that magnetic flux density 'B' at the centre of a current carrying circular coil of radius R is given by: `B = ("μ"_0I)/(2R)` where the terms have their usual meaning.
उत्तर
Let a circular coil of radius R carry a current I and O be its centre.
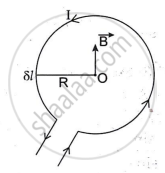
By Biot-Savart's law, the magnitude of the magnetic field at O due a small element δ l of the loop is,
`δB = "μ"_0/(4π) (Iδl sinθ)/R^2`
Where θ is the angle between the length of the element (δ l) and the line joining the element to the point O. Here, θ = 90° because every element of. a circle is perpendicular to the radius.
∴ `δB = "μ"_0/(4π) (Iδl)/R^2`
Every component of the coil will have the same field direction. Because of the complete coil, the field `vec B` magnitude at O is:
`B = "μ"_0/(4pi)I/R^2 "∑"δl`
But `"∑ "δl = 2piR`
∴ `B = "μ"_0/(4pi) · I/R^2 xx 2piR`
or `B = ("μ"_0I)/(2R)`
APPEARS IN
संबंधित प्रश्न
State Biot – Savart law.
What does a toroid consist of? Find out the expression for the magnetic field inside a toroid for N turns of the coil having the average radius r and carrying a current I. Show that the magnetic field in the open space inside and exterior to the toroid is zero.
An alpha particle is projected vertically upward with a speed of 3.0 × 104 km s−1 in a region where a magnetic field of magnitude 1.0 T exists in the direction south to north. Find the magnetic force that acts on the α-particle.
The magnetic field at the origin due to a current element \[i d \vec{l}\] placed at a position \[\vec{r}\] is
(a)\[\frac{\mu_0 i}{4\pi}\frac{d \vec{l} \times \vec{r}}{r^3}\]
(b) \[- \frac{\mu_0 i}{4\pi}\frac{\vec{r} \times d \vec{l}}{r^3}\]
(c) \[\frac{\mu_0 i}{4\pi}\frac{\vec{r} \times d \vec{l}}{r^3}\]
(d) \[- \frac{\mu_0 i}{4\pi}\frac{d \vec{l} \times \vec{r}}{r^3}\]
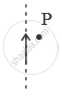
An electric current I flows through an infinitely long conductor as shown in Figure 2 (a) below. Write an expression and direction for the magnetic field at point P.
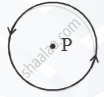
An electric current I flows through a circular loop as shown in Figure 2(b) below. Write an expression and direction for the magnetic field at the centre of the loop at point P.
State Biot Savart law.
State and explain the law used to determine the magnetic field at a point due to a current element. Derive the expression for the magnetic field due to a circular current-carrying loop of radius r at its center.
- both are long range and inversely proportional to the square of distance from the source to the point of interest.
-
both are linear in source.
-
both are produced by scalar sources.
-
both follow principle of superposition.
The magnetic field at any point on the axis of a current element is ______
