Advertisements
Advertisements
प्रश्न
What does a toroid consist of? Find out the expression for the magnetic field inside a toroid for N turns of the coil having the average radius r and carrying a current I. Show that the magnetic field in the open space inside and exterior to the toroid is zero.
उत्तर
Toroid is a hollow circular ring on which a large number of turns of a wire are closely wound.
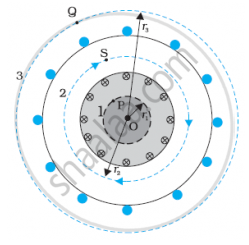
Figure shows a sectional view of the toroid. The direction of the magnetic field inside is clockwise as per the right-hand thumb rule for circular loops. Three circular Amperian loops 1, 2 and 3 are shown by dashed lines.
By symmetry, the magnetic field should be tangential to each of them and constant in magnitude for a given loop.
Let the magnetic field inside the toroid be B. We shall now consider the magnetic field at S. Once again we employ
Ampere’s law in the form of,
`ointvecB.dvecI = μ_0I` Or, BL = μ0NI
Where, L is the length of the loop for which B is tangential, I be the current enclosed by the loop and N be the number of turns.
We find, L = 2πr.
The current enclosed I is (for N turns of toroidal coil) N I.
B (2πr) = µ0NI , therefore, `B = (μ_0NI)/(2pir)`
Open space inside the toroid encloses no current thus, I = 0.
Hence, B = 0
Open space exterior to the toroid:
Each turn of current carrying wire is cut twice by the loop 3. Thus, the current coming out of the plane of the paper is cancelled exactly by the current going into it. Thus,
I= 0, and B = 0.
APPEARS IN
संबंधित प्रश्न
Using Biot − Savart’s law, derive the expression for the magnetic field in the vector form at a point on the axis of a circular current loop?
A wire of length l is bent in the form of an equilateral triangle and carries an electric current i. (a) Find the magnetic field B at the centre. (b) If the wire is bent in the form of a square, what would be the value of B at the centre?
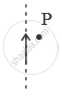
An electric current I flows through an infinitely long conductor as shown in Figure 2 (a) below. Write an expression and direction for the magnetic field at point P.
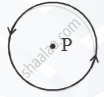
An electric current I flows through a circular loop as shown in Figure 2(b) below. Write an expression and direction for the magnetic field at the centre of the loop at point P.
State and explain the law used to determine magnetic field at a point due to a current element. Derive the expression for the magnetic field due to a circular current carrying loop of radius r at its centre.
A straight wire carrying a current of 5 A is bent into a semicircular arc of radius 2 cm as shown in the figure. Find the magnitude and direction of the magnetic field at the centre of the arc.

State and explain the law used to determine the magnetic field at a point due to a current element. Derive the expression for the magnetic field due to a circular current-carrying loop of radius r at its center.
A square shaped current carrying loop MNOP is placed near a straight long current carrying wire AB as shown in the fig. The wire and the loop lie in the same plane. If the loop experiences a net force F towards the wire, find the magnitude of the force on the side 'NO' of the loop.

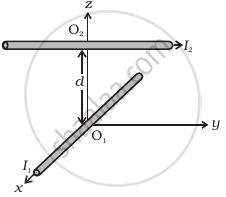
Two long wires carrying current I1 and I2 are arranged as shown in figure. The one carrying current I1 is along is the x-axis. The other carrying current I2 is along a line parallel to the y-axis given by x = 0 and z = d. Find the force exerted at O2 because of the wire along the x-axis.