Advertisements
Advertisements
प्रश्न
Using Biot − Savart’s law, derive the expression for the magnetic field in the vector form at a point on the axis of a circular current loop?
उत्तर
Magnetic field on the axis of a circular current loop
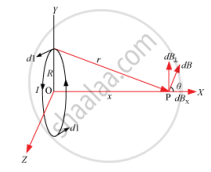
I →Current in the loop, R →Radii of the loop, X-axis →Axis of the loop, x →Distance of OP
dl →Conducting element of the loop
According to Biot-Savart’s law, the magnetic field at P is `dB =(μ_0I|dI xx r)/(4pir^3)`
r2 = x2+ R2
| dl × r | = r dl (∵ they are perpendicular)
`thereforedB = (μ_0)/(4pi) (IdI)/((x^2 +R^2))`
dB has two components − dBx and dB⊥. dB⊥ is cancelled out and only the x-component remains.
∴ dBx= dBcosθ
`Cos theta = R/((x^2 + R^2)^(1/2)`
`therefore dB_x =(μ_0IdI)/(4pi) R/(x^2 +R^2)^(3/2)`
Summation of dl over the loop is given by 2πR.
`B =B_xhati =(μ_0IR^2)/(2(x^2 + R^2)^(3/2 ) )hati`
APPEARS IN
संबंधित प्रश्न
An alpha particle is projected vertically upward with a speed of 3.0 × 104 km s−1 in a region where a magnetic field of magnitude 1.0 T exists in the direction south to north. Find the magnetic force that acts on the α-particle.
A long, vertical wire carrying a current of 10 A in the upward direction is placed in a region where a horizontal magnetic field of magnitude 2.0 × 10−3 T exists from south to north. Find the point where the resultant magnetic field is zero.
A wire of length l is bent in the form of an equilateral triangle and carries an electric current i. (a) Find the magnetic field B at the centre. (b) If the wire is bent in the form of a square, what would be the value of B at the centre?
A wire of length l is bent in the form of an equilateral triangle and carries an electric current i. Find the magnetic field B at the centre.
A regular polygon of n sides is formed by bending a wire of total length 2πr which carries a current i. (a) Find the magnetic filed B at the centre of the polygon. (b) By letting n → ∞, deduce the expression for the magnetic field at the centre of a circular current.
State and explain the law used to determine magnetic field at a point due to a current element. Derive the expression for the magnetic field due to a circular current carrying loop of radius r at its centre.
A long wire with a small current element of length 1 cm is placed at the origin and carries a current of 10 A along the X-axis. Find out the magnitude and direction of the magnetic field due to the element on the Y-axis at a distance 0.5 m from it.
Derive the expression for the magnetic field due to a current carrying coil of radius r at a distance x from the centre along the X-axis.
Two concentric circular loops of radius 1 cm and 20 cm are placed coaxially.
(i) Find mutual inductance of the arrangement.
(ii) If the current passed through the outer loop is changed at a rate of 5 A/ms, find the emf induced in the inner loop. Assume the magnetic field on the inner loop to be uniform.
The magnetic field at any point on the axis of a current element is ______
