Advertisements
Advertisements
प्रश्न
State and explain the law used to determine magnetic field at a point due to a current element. Derive the expression for the magnetic field due to a circular current carrying loop of radius r at its centre.
उत्तर
The law which gives the magnetic field at a point due to a current element, is Biot-Savart Law.
It states that,if we consider an infinitesimal element dl of the
conductor,the magnetic field dB due to this
element can be determined at a point P at a distance r from it, as follows:
Let θ be the angle between dl and the displacement vector r.
According to Biot-Savart’s law,the magnitude of the magnetic field dB is proportional tothe current I, the element length |dl|,and inversely proportional to the square of the distance r. Its direction is perpendicular to the plane containing dl and r .
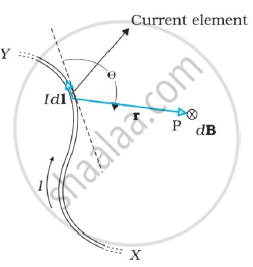
Thus, in vector notation, `d vec( B ) α I (d vec (l)xx vec(r))/(r^3)`
where μ0 / 4π is a constant of proportionality. The above expression holds when the medium is vacuum.The magnitude of this field is,
`|d vec(B) | = (mu_0)/(4pi) (Idlsin theta )/(r^2)`
The proportionality constant in SI units has the exact value,
`(mu_0)/(4pi) = 10^(-7) T - m/A`
We call μ0 the permeability of free space (or vacuum).
Magnetic field at the centre of a circular loop of radius r carrying current I:
We consider a small element of length dl. The `vec (r)` joining the centre of the circle to this element is perpendicular to`d vec(l)` . Hence the magnitude of magnetic field at the centre due to this element (by Biot-Savart Law) is
`dB = (mu_0)/(4 pi) (Idl sin theta)/(r^2) or dB= (mu_0)/(4 pi) (Idl sin 90^circ)/(r^2) = (mu_0)/(4pi) (Idl)/(r^2)`
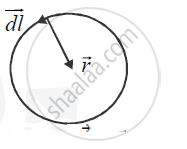
This field is perpendicular to the plane of the coil (as it is directed along `dvec(l) xx vec (r))`.
Hence, net field due to the entire circular loop, is
`B = int (mu_0)/(4 pi) (Idl )/(r^2) = (mu_0)/(4 pi) (I)/(r^2) int dl = (mu_0)/(4 pi) xx(I)/(r^2) xx 2 pir`
Or B = `(mu_0I)/(2r)`
APPEARS IN
संबंधित प्रश्न
A proton goes undeflected in a crossed electric and magnetic field (the fields are perpendicular to each other) at a speed of 2.0 × 105 m s−1. The velocity is perpendicular to both the fields. When the electric field is switched off, the proton moves along a circle of radius 4.0 cm. Find the magnitudes of the electric and magnetic fields. Take the mass of the proton = 1.6 × 10−27 kg
A wire of length l is bent in the form of an equilateral triangle and carries an electric current i. (a) Find the magnetic field B at the centre. (b) If the wire is bent in the form of a square, what would be the value of B at the centre?
A wire of length l is bent in the form of an equilateral triangle and carries an electric current i. Find the magnetic field B at the centre.
A straight wire carrying a current of 5 A is bent into a semicircular arc of radius 2 cm as shown in the figure. Find the magnitude and direction of the magnetic field at the centre of the arc.

State and explain the law used to determine the magnetic field at a point due to a current element. Derive the expression for the magnetic field due to a circular current-carrying loop of radius r at its center.
Biot-Savart law indicates that the moving electrons (velocity v) produce a magnetic field B such that ______.
A circular loop of radius 0.3 cm lies parallel to much bigger circular of radius 20 cm. The centre of the small loop is on the axis of the bigger loop. The distance between their centres is 15 cm. If a current of 2.0 A flows through the smaller loop, then the flux linked with the bigger loop is ______.
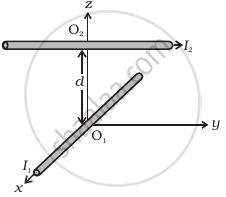
Two long wires carrying current I1 and I2 are arranged as shown in figure. The one carrying current I1 is along is the x-axis. The other carrying current I2 is along a line parallel to the y-axis given by x = 0 and z = d. Find the force exerted at O2 because of the wire along the x-axis.
A current carrying loop consists of 3 identical quarter circles of radius R, lying in the positive quadrants of the x-y, y-z and z-x planes with their centres at the origin, joined together. Find the direction and magnitude of B at the origin.
