Advertisements
Advertisements
Question
State and explain the law used to determine magnetic field at a point due to a current element. Derive the expression for the magnetic field due to a circular current carrying loop of radius r at its centre.
Solution
The law which gives the magnetic field at a point due to a current element, is Biot-Savart Law.
It states that,if we consider an infinitesimal element dl of the
conductor,the magnetic field dB due to this
element can be determined at a point P at a distance r from it, as follows:
Let θ be the angle between dl and the displacement vector r.
According to Biot-Savart’s law,the magnitude of the magnetic field dB is proportional tothe current I, the element length |dl|,and inversely proportional to the square of the distance r. Its direction is perpendicular to the plane containing dl and r .
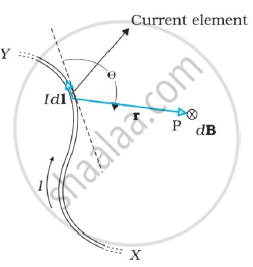
Thus, in vector notation, `d vec( B ) α I (d vec (l)xx vec(r))/(r^3)`
where μ0 / 4π is a constant of proportionality. The above expression holds when the medium is vacuum.The magnitude of this field is,
`|d vec(B) | = (mu_0)/(4pi) (Idlsin theta )/(r^2)`
The proportionality constant in SI units has the exact value,
`(mu_0)/(4pi) = 10^(-7) T - m/A`
We call μ0 the permeability of free space (or vacuum).
Magnetic field at the centre of a circular loop of radius r carrying current I:
We consider a small element of length dl. The `vec (r)` joining the centre of the circle to this element is perpendicular to`d vec(l)` . Hence the magnitude of magnetic field at the centre due to this element (by Biot-Savart Law) is
`dB = (mu_0)/(4 pi) (Idl sin theta)/(r^2) or dB= (mu_0)/(4 pi) (Idl sin 90^circ)/(r^2) = (mu_0)/(4pi) (Idl)/(r^2)`
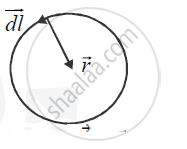
This field is perpendicular to the plane of the coil (as it is directed along `dvec(l) xx vec (r))`.
Hence, net field due to the entire circular loop, is
`B = int (mu_0)/(4 pi) (Idl )/(r^2) = (mu_0)/(4 pi) (I)/(r^2) int dl = (mu_0)/(4 pi) xx(I)/(r^2) xx 2 pir`
Or B = `(mu_0I)/(2r)`
APPEARS IN
RELATED QUESTIONS
What does a toroid consist of? Find out the expression for the magnetic field inside a toroid for N turns of the coil having the average radius r and carrying a current I. Show that the magnetic field in the open space inside and exterior to the toroid is zero.
Derive the expression for the magnetic field due to a current carrying coil of radius r at a distance x from the centre along the X-axis.
A straight wire carrying a current of 5 A is bent into a semicircular arc of radius 2 cm as shown in the figure. Find the magnitude and direction of the magnetic field at the centre of the arc.

State Biot Savart law.
State and explain the law used to determine the magnetic field at a point due to a current element. Derive the expression for the magnetic field due to a circular current-carrying loop of radius r at its center.
A square shaped current carrying loop MNOP is placed near a straight long current carrying wire AB as shown in the fig. The wire and the loop lie in the same plane. If the loop experiences a net force F towards the wire, find the magnitude of the force on the side 'NO' of the loop.

Biot-Savart law indicates that the moving electrons (velocity v) produce a magnetic field B such that ______.
- both are long range and inversely proportional to the square of distance from the source to the point of interest.
-
both are linear in source.
-
both are produced by scalar sources.
-
both follow principle of superposition.
Biot-Savart law indicates that the moving electrons velocity (V) produce a magnetic field B such that ______.
Two identical circular loops P and Q, each of radius R carrying current I are kept in perpendicular planes such that they have a common centre O as shown in the figure.
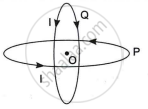
Find the magnitude and direction of the net magnetic field at point O.
