Advertisements
Advertisements
Question
State and explain the law used to determine the magnetic field at a point due to a current element. Derive the expression for the magnetic field due to a circular current-carrying loop of radius r at its center.
Solution
The magnetic field at a certain point due to an element of a current-carrying conductor is given by Biot Savart's law. According to Biot-Savart’s law, the magnitude of the magnetic field dB due to a current-carrying element of length |dl| at a distance r is proportional to the current I, length of the element |dl|, and inversely proportional to the square of the distance r. Its direction is perpendicular to the plane containing dl and r.
Thus, in vector notation,
` "dB" alpha (vec("idl") xx vec("r"))/"r"^3 `
`"dB" = mu_° /(4pi) (vec("idl") xx "r")/"r"^3`
Magnetic field due to a circular current carrying loop:
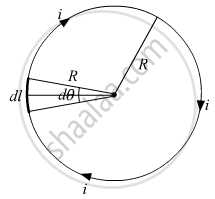
Let the current in the circular loop of radius R is i, now if take a small element of the loop, dl, making an angle dθ at the center.
The magnetic field at the center by using Biot-Savart law is, `vec"dB" = mu_°/(4pi) (vec"idl" xx vec"R")/("R"^3) = mu_°/(4pi) ("idl")/"R"^2 hat"n"` ...`(vec"dl" ⊥ vec"R", hat"n" ⊥ vec "dl"& vec"R")`
∵ dl = rdθ
⇒ `|vec"dB"| = mu_° /(4pi) ("Rd"theta)/R^2 = (mu_°"i")/(4pi"R")"d"theta`
⇒ `|vec"B"| = mu_° /(4pi"R") int_0^(2pi) "d"theta = (mu_°"i")/(2"R")`
⇒ `|vec"B"| = (mu_°"i")/(2"R")`
⇒ `vec"B" = (mu_°"i")/(2"R") hat"n"` ....(Where `hat"n"` is a vector perpendicular to the plane of loop, directed downward)
APPEARS IN
RELATED QUESTIONS
What does a toroid consist of? Find out the expression for the magnetic field inside a toroid for N turns of the coil having the average radius r and carrying a current I. Show that the magnetic field in the open space inside and exterior to the toroid is zero.
A proton goes undeflected in a crossed electric and magnetic field (the fields are perpendicular to each other) at a speed of 2.0 × 105 m s−1. The velocity is perpendicular to both the fields. When the electric field is switched off, the proton moves along a circle of radius 4.0 cm. Find the magnitudes of the electric and magnetic fields. Take the mass of the proton = 1.6 × 10−27 kg
A long, vertical wire carrying a current of 10 A in the upward direction is placed in a region where a horizontal magnetic field of magnitude 2.0 × 10−3 T exists from south to north. Find the point where the resultant magnetic field is zero.
A wire of length l is bent in the form of an equilateral triangle and carries an electric current i. Find the magnetic field B at the centre.
A regular polygon of n sides is formed by bending a wire of total length 2πr which carries a current i. (a) Find the magnetic filed B at the centre of the polygon. (b) By letting n → ∞, deduce the expression for the magnetic field at the centre of a circular current.
State and explain the law used to determine magnetic field at a point due to a current element. Derive the expression for the magnetic field due to a circular current carrying loop of radius r at its centre.
Two concentric circular loops of radius 1 cm and 20 cm are placed coaxially.
(i) Find mutual inductance of the arrangement.
(ii) If the current passed through the outer loop is changed at a rate of 5 A/ms, find the emf induced in the inner loop. Assume the magnetic field on the inner loop to be uniform.
Biot-Savart law indicates that the moving electrons velocity (V) produce a magnetic field B such that ______.
A circular loop of radius 0.3 cm lies parallel to much bigger circular of radius 20 cm. The centre of the small loop is on the axis of the bigger loop. The distance between their centres is 15 cm. If a current of 2.0 A flows through the smaller loop, then the flux linked with the bigger loop is ______.
Using Biot-Savart law, show that magnetic flux density 'B' at the centre of a current carrying circular coil of radius R is given by: `B = ("μ"_0I)/(2R)` where the terms have their usual meaning.
