Advertisements
Advertisements
Question
A long wire with a small current element of length 1 cm is placed at the origin and carries a current of 10 A along the X-axis. Find out the magnitude and direction of the magnetic field due to the element on the Y-axis at a distance 0.5 m from it.
Solution
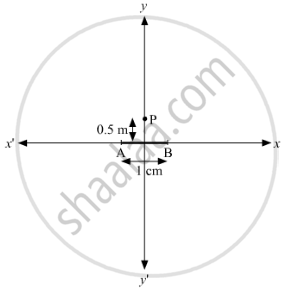
`vec|dB| = (mu_0)/(4 pi) (I dl sin theta ) / (r^2) `
dl = Δx = 10-2 m , I = 10A r = 0.5 m = y, `mu_0 /4 pi = 10^(-7) (Tm)/A`
`theta = 90^circ ; sin theta = 1 `
`vec|dB| = (10^(-7) xx 10 xx 10^(-2))/(25 xx 10^(-2)) = 4 xx 10^(-8) T`
The direction of the field is in the + z-direction. This is so since,
`vec(dl) xx vec(r) = Delta x hat (i) xx y hat (j) = y Delta x ( hat(i) xx hat(j) ) = y Delta x hat (k)`
Hence the direction of magnetic field is towards positive z-axis.
RELATED QUESTIONS
State Biot-Savart law.
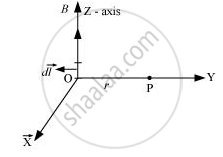
A current I flows in a conductor placed perpendicular to the plane of the paper. Indicate the direction of the magnetic field due to a small element d `vecl` at point P situated at distance `vecr` from the element as shown in the figure.
The magnetic field at the origin due to a current element \[i d \vec{l}\] placed at a position \[\vec{r}\] is
(a)\[\frac{\mu_0 i}{4\pi}\frac{d \vec{l} \times \vec{r}}{r^3}\]
(b) \[- \frac{\mu_0 i}{4\pi}\frac{\vec{r} \times d \vec{l}}{r^3}\]
(c) \[\frac{\mu_0 i}{4\pi}\frac{\vec{r} \times d \vec{l}}{r^3}\]
(d) \[- \frac{\mu_0 i}{4\pi}\frac{d \vec{l} \times \vec{r}}{r^3}\]
A regular polygon of n sides is formed by bending a wire of total length 2πr which carries a current i. (a) Find the magnetic filed B at the centre of the polygon. (b) By letting n → ∞, deduce the expression for the magnetic field at the centre of a circular current.
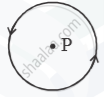
An electric current I flows through a circular loop as shown in Figure 2(b) below. Write an expression and direction for the magnetic field at the centre of the loop at point P.
State Biot Savart law.
A square shaped current carrying loop MNOP is placed near a straight long current carrying wire AB as shown in the fig. The wire and the loop lie in the same plane. If the loop experiences a net force F towards the wire, find the magnitude of the force on the side 'NO' of the loop.

Two concentric circular loops of radius 1 cm and 20 cm are placed coaxially.
(i) Find mutual inductance of the arrangement.
(ii) If the current passed through the outer loop is changed at a rate of 5 A/ms, find the emf induced in the inner loop. Assume the magnetic field on the inner loop to be uniform.
Biot-Savart law indicates that the moving electrons velocity (V) produce a magnetic field B such that ______.
Using Biot-Savart law, show that magnetic flux density 'B' at the centre of a current carrying circular coil of radius R is given by: `B = ("μ"_0I)/(2R)` where the terms have their usual meaning.
