Advertisements
Advertisements
Question
Using Biot-Savart law, show that magnetic flux density 'B' at the centre of a current carrying circular coil of radius R is given by: `B = ("μ"_0I)/(2R)` where the terms have their usual meaning.
Solution
Let a circular coil of radius R carry a current I and O be its centre.
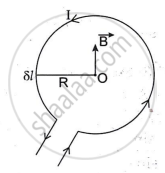
By Biot-Savart's law, the magnitude of the magnetic field at O due a small element δ l of the loop is,
`δB = "μ"_0/(4π) (Iδl sinθ)/R^2`
Where θ is the angle between the length of the element (δ l) and the line joining the element to the point O. Here, θ = 90° because every element of. a circle is perpendicular to the radius.
∴ `δB = "μ"_0/(4π) (Iδl)/R^2`
Every component of the coil will have the same field direction. Because of the complete coil, the field `vec B` magnitude at O is:
`B = "μ"_0/(4pi)I/R^2 "∑"δl`
But `"∑ "δl = 2piR`
∴ `B = "μ"_0/(4pi) · I/R^2 xx 2piR`
or `B = ("μ"_0I)/(2R)`
APPEARS IN
RELATED QUESTIONS
Express Biot – Savart law in the vector form.
State Biot-Savart law.
A current I flows in a conductor placed perpendicular to the plane of the paper. Indicate the direction of the magnetic field due to a small element d `vecl` at point P situated at distance `vecr` from the element as shown in the figure.
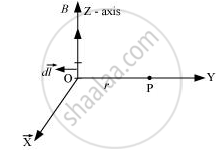
The magnetic field at the origin due to a current element \[i d \vec{l}\] placed at a position \[\vec{r}\] is
(a)\[\frac{\mu_0 i}{4\pi}\frac{d \vec{l} \times \vec{r}}{r^3}\]
(b) \[- \frac{\mu_0 i}{4\pi}\frac{\vec{r} \times d \vec{l}}{r^3}\]
(c) \[\frac{\mu_0 i}{4\pi}\frac{\vec{r} \times d \vec{l}}{r^3}\]
(d) \[- \frac{\mu_0 i}{4\pi}\frac{d \vec{l} \times \vec{r}}{r^3}\]
A regular polygon of n sides is formed by bending a wire of total length 2πr which carries a current i. (a) Find the magnetic filed B at the centre of the polygon. (b) By letting n → ∞, deduce the expression for the magnetic field at the centre of a circular current.
Derive the expression for the magnetic field due to a current carrying coil of radius r at a distance x from the centre along the X-axis.
State and explain the law used to determine the magnetic field at a point due to a current element. Derive the expression for the magnetic field due to a circular current-carrying loop of radius r at its center.
A square shaped current carrying loop MNOP is placed near a straight long current carrying wire AB as shown in the fig. The wire and the loop lie in the same plane. If the loop experiences a net force F towards the wire, find the magnitude of the force on the side 'NO' of the loop.

Biot-Savart law indicates that the moving electrons (velocity v) produce a magnetic field B such that ______.
Biot-Savart law indicates that the moving electrons velocity (V) produce a magnetic field B such that ______.
A current carrying loop consists of 3 identical quarter circles of radius R, lying in the positive quadrants of the x-y, y-z and z-x planes with their centres at the origin, joined together. Find the direction and magnitude of B at the origin.
