Advertisements
Advertisements
Question
Express Biot – Savart law in the vector form.
Solution
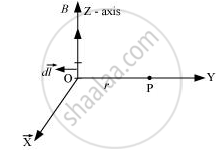
Consider a straight infinnitely long wire carrying a steady current I. Point P is the perpenicular distance from the wire. Consider a small element dl of the wire at the point O on the wire. The line joining points O to P( OP = vector r ) makes an angle θ with the direction of the current element dl.

`dvecB = (μ_oI)/(4π) (vec(dl) xx vec r)/r^3`
The expression for the total magnetic field B due to the wire can be obtained by intergrating the above expression as
`vecB =∫(μ_oI)/(4π) (vec(dl)xxvecr)/r^3`
It is the biot savart law which gives the magnetic field B generated by steady electric current I when the current can be approximated as running through an infinitely running wire.
RELATED QUESTIONS
State Biot-Savart law.
A current I flows in a conductor placed perpendicular to the plane of the paper. Indicate the direction of the magnetic field due to a small element d `vecl` at point P situated at distance `vecr` from the element as shown in the figure.
A long, vertical wire carrying a current of 10 A in the upward direction is placed in a region where a horizontal magnetic field of magnitude 2.0 × 10−3 T exists from south to north. Find the point where the resultant magnetic field is zero.
A wire of length l is bent in the form of an equilateral triangle and carries an electric current i. Find the magnetic field B at the centre.
A regular polygon of n sides is formed by bending a wire of total length 2πr which carries a current i. (a) Find the magnetic filed B at the centre of the polygon. (b) By letting n → ∞, deduce the expression for the magnetic field at the centre of a circular current.
Derive the expression for the magnetic field due to a current carrying coil of radius r at a distance x from the centre along the X-axis.
A straight wire carrying a current of 5 A is bent into a semicircular arc of radius 2 cm as shown in the figure. Find the magnitude and direction of the magnetic field at the centre of the arc.

A straight wire carrying a current of 5 A is bent into a semicircular arc radius 2 cm as shown in the figure. Find the magnitude and direction of the magnetic field at the center of the arc

- both are long range and inversely proportional to the square of distance from the source to the point of interest.
-
both are linear in source.
-
both are produced by scalar sources.
-
both follow principle of superposition.
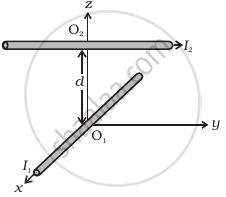
Two long wires carrying current I1 and I2 are arranged as shown in figure. The one carrying current I1 is along is the x-axis. The other carrying current I2 is along a line parallel to the y-axis given by x = 0 and z = d. Find the force exerted at O2 because of the wire along the x-axis.