Advertisements
Advertisements
Question
Derive the expression for the magnetic field due to a current carrying coil of radius r at a distance x from the centre along the X-axis.
Solution
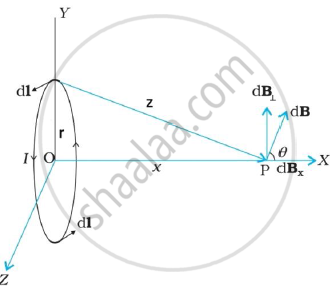
Figure depicts a circular loop carrying a steadycurrent I. The loop is placed in the y-z plane with its centre at the origin O and has a radius R. The x-axis is the axis of the loop. We wish to calculate the magnetic field at the point P on this axis. Let x be the distance of P from the centre O of the loop.
Consider a conducting element dl of the loop. This is shown in the igure. The magnitude dB of the magnetic field due to dl is given by the Biot-Savart law,
`dB = (mu_0)/(4pi) (I|vec(dl) xx vec(z)|)/(z^3) ` ——— (i)
Now z2 = x2 + r2 .
Further, any element of the loop will be perpendicular to the displacement vector from the element to the axial point. For example, the element dl in the figure is in the y-z plane whereas the displacement vector r from dl to the axial point P is in the x-y plane.
Hence `|dvec(l) xx vec(z) |` = z d1 Thus,
`dB = (mu_0)/(4 pi) (Idl)/((x^2 + r^2))`——— (ii)
The direction of dB is shown in the figure. It is perpendicular to the plane formed by`vec(dl) ` and `vec(r)`.has an x - component d`vec(B)_x` and a component perpendicular to x-axis, `vec(dB)_⊥` . When the components perpendicular to the x-axis are summed over, they cancel out and we obtain a null result.
For example, the dB⊥ .component due to dl is cancelled by thecontribution due to the diametrically opposite dl element, shown in figure. Thus, only the x-component survives. The net contributionalong xdirection can be obtained by integrating dBx = dB cos θ over theloop. For the figure,
`cos theta = r/((x^2 + r^2 )^(1/2)`——— (iii)
From Eqs. (ii) and (iii),
`dB_x = (mu_0)/(4pi) I.dl r /((x^2 + r^2)3/2`
The summation of elements dl over the loop yields 2πr, the circumference of the loop. Thus, the magnetic field at P due to entire circular loop is
`vec(B) = B_xhat(i) = (mu_0 Ir^2)/(2(x^2 +r^2)3/2) hat(i)`
APPEARS IN
RELATED QUESTIONS
What does a toroid consist of? Find out the expression for the magnetic field inside a toroid for N turns of the coil having the average radius r and carrying a current I. Show that the magnetic field in the open space inside and exterior to the toroid is zero.
The magnetic field at the origin due to a current element \[i d \vec{l}\] placed at a position \[\vec{r}\] is
(a)\[\frac{\mu_0 i}{4\pi}\frac{d \vec{l} \times \vec{r}}{r^3}\]
(b) \[- \frac{\mu_0 i}{4\pi}\frac{\vec{r} \times d \vec{l}}{r^3}\]
(c) \[\frac{\mu_0 i}{4\pi}\frac{\vec{r} \times d \vec{l}}{r^3}\]
(d) \[- \frac{\mu_0 i}{4\pi}\frac{d \vec{l} \times \vec{r}}{r^3}\]
A regular polygon of n sides is formed by bending a wire of total length 2πr which carries a current i. (a) Find the magnetic filed B at the centre of the polygon. (b) By letting n → ∞, deduce the expression for the magnetic field at the centre of a circular current.
An electric current I flows through an infinitely long conductor as shown in Figure 2 (a) below. Write an expression and direction for the magnetic field at point P.
State and explain the law used to determine magnetic field at a point due to a current element. Derive the expression for the magnetic field due to a circular current carrying loop of radius r at its centre.
A straight wire carrying a current of 5 A is bent into a semicircular arc radius 2 cm as shown in the figure. Find the magnitude and direction of the magnetic field at the center of the arc

A square shaped current carrying loop MNOP is placed near a straight long current carrying wire AB as shown in the fig. The wire and the loop lie in the same plane. If the loop experiences a net force F towards the wire, find the magnitude of the force on the side 'NO' of the loop.

A circular loop of radius 0.3 cm lies parallel to much bigger circular of radius 20 cm. The centre of the small loop is on the axis of the bigger loop. The distance between their centres is 15 cm. If a current of 2.0 A flows through the smaller loop, then the flux linked with the bigger loop is ______.
Using Biot-Savart law, show that magnetic flux density 'B' at the centre of a current carrying circular coil of radius R is given by: `B = ("μ"_0I)/(2R)` where the terms have their usual meaning.
