Advertisements
Advertisements
Question
An electric current I flows through an infinitely long conductor as shown in Figure 2 (a) below. Write an expression and direction for the magnetic field at point P.
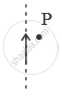
Solution
`therefore` By Biot savart’s law
`vec(B) = ∫ vec (dB) = mu_0/(4pi) ∫ (I vec(dl) xx vec(r))/r^3`
The magnetic field created by a current carrying wire is radial magnetic field.
APPEARS IN
RELATED QUESTIONS
Express Biot – Savart law in the vector form.
The magnetic field at the origin due to a current element \[i d \vec{l}\] placed at a position \[\vec{r}\] is
(a)\[\frac{\mu_0 i}{4\pi}\frac{d \vec{l} \times \vec{r}}{r^3}\]
(b) \[- \frac{\mu_0 i}{4\pi}\frac{\vec{r} \times d \vec{l}}{r^3}\]
(c) \[\frac{\mu_0 i}{4\pi}\frac{\vec{r} \times d \vec{l}}{r^3}\]
(d) \[- \frac{\mu_0 i}{4\pi}\frac{d \vec{l} \times \vec{r}}{r^3}\]
A proton goes undeflected in a crossed electric and magnetic field (the fields are perpendicular to each other) at a speed of 2.0 × 105 m s−1. The velocity is perpendicular to both the fields. When the electric field is switched off, the proton moves along a circle of radius 4.0 cm. Find the magnitudes of the electric and magnetic fields. Take the mass of the proton = 1.6 × 10−27 kg
State and explain the law used to determine magnetic field at a point due to a current element. Derive the expression for the magnetic field due to a circular current carrying loop of radius r at its centre.
A long wire with a small current element of length 1 cm is placed at the origin and carries a current of 10 A along the X-axis. Find out the magnitude and direction of the magnetic field due to the element on the Y-axis at a distance 0.5 m from it.
Derive the expression for the magnetic field due to a current carrying coil of radius r at a distance x from the centre along the X-axis.
Derive the expression for the magnetic field due to a current-carrying coil of radius r at a distance x from the center along the X-axis.
Two concentric circular loops of radius 1 cm and 20 cm are placed coaxially.
(i) Find mutual inductance of the arrangement.
(ii) If the current passed through the outer loop is changed at a rate of 5 A/ms, find the emf induced in the inner loop. Assume the magnetic field on the inner loop to be uniform.
The magnetic field at any point on the axis of a current element is ______
